【題目】已知二次函數
， 
.
（1）若
，寫出函數的單調增區間和減區間；
（2）若
，求函數的最大值和最小值；
（3）若函數在
上是單調函數，求實數
的取值范圍.
科目：高中數學 來源： 題型：
【題目】公元
年左右，我國數學家劉徽發現當圓內接正多邊形的邊數無限增加時，多邊形的面積可無限逼近圓的面積，并創立了“割圓術”劉徽得到了圓周率精確到小數點后兩位的近似值
，這就是著名的“徽率”.如圖是利用劉徽的“割圓術”思想設計的一個程序框圖，其中
表示圓內接正多邊形的邊數，執行此算法輸出的圓周率的近似值依次為 （ ）
（參考數據： 
）
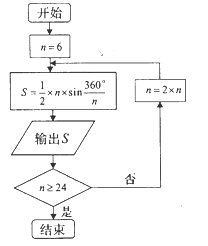
A. 2.598,3,3.1048 B. 2.598,3,3.1056
C. 2.578,3,3.1069 D. 2.588,3,3.1108
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數
（
為常數，
=2.71828……是自然對數的底數），曲線
在點
處的切線與
軸平行．
（1）求的值；
（2）求
的單調區間；
（3）設
，其中
是的導函數．證明：對任意
＞0，
＜
．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】在多面體ABCDEF中，底面ABCD是梯形，四邊形ADEF是正方形，AB∥DC，AB＝AD＝1，CD＝2，AC＝EC＝
。
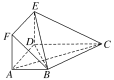
(1)求證：平面EBC⊥平面EBD；
(2)設M為線段EC上一點，且3EM＝EC，試問在線段BC上是否存在一點T，使得MT∥平面BDE，若存在，試指出點T的位置；若不存在，請說明理由．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】否定“自然數
、
、
中恰有一個偶數”時正確的反設為（ ）
A. 
、
、
都是奇數 B. 
、
、
至少有兩個偶數
C. 
、
、
都是偶數 D. 
、
、
中都是奇數或至少有兩個偶數
查看答案和解析>>
科目：高中數學 來源： 題型：
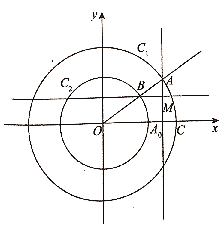
【題目】如圖所示，以原點
為圓心的兩個同心圓
，其中，大圓
的半徑為
，小圓的半徑為
，點
為大圓
上一動點，連接
，與小圓
交于點
，過點
作
軸的垂線，垂足為
，過點
作直線
的垂線，垂足為
，點
，記
.
（1）求點
的坐標（用含有
的式子表示），并寫出點
的軌跡方程，指出點
的軌跡是什么曲線；
（2）設點
的軌跡為
，點
分別是曲線
上的兩個動點，且
，求
的值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
