
(1)設 ,若矩陣A=
,若矩陣A= 的變換把直線
的變換把直線 變換為另一直線
變換為另一直線 .
.
(1)求 的值;
的值;
(2)求矩陣A的特征值.
(1)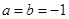 ;(2)矩陣A的特征值
;(2)矩陣A的特征值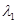 =
=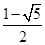 ,
,
 .
.
解析試題分析:本題主要考查矩陣的變換、特征矩陣、特征多項式、特征值等基礎知識,考查學生的轉化能力、計算能力.第一問,設出直線上的點P,直線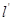 上的點
上的點 點坐標,列出矩陣變換的表達式,得到等量關系,將得到的點
點坐標,列出矩陣變換的表達式,得到等量關系,將得到的點 坐標代入直線
坐標代入直線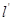 上,得到x與y的關系式,與直線l相對比,得到等量關系,解出a和b;第二問,結合(1)的結論,先得到矩陣A寫出特征矩陣,計算出特征多項式
上,得到x與y的關系式,與直線l相對比,得到等量關系,解出a和b;第二問,結合(1)的結論,先得到矩陣A寫出特征矩陣,計算出特征多項式 ,通過
,通過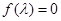 得到矩陣A的特征值.
得到矩陣A的特征值.
試題解析:(1)設直線 上的任一點
上的任一點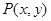 在變換作用下變成了
在變換作用下變成了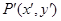 ,
,
則有 ,
,
即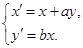 1分
1分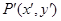 在直線
在直線 上,
上,
所以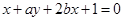 ,
,
即 , 2
, 2
所以 
所以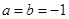 . 4分
. 4分
(2)由(1)知矩陣A=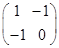 ,
,
特征矩陣為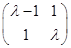 . 5分
. 5分
特征多項式為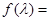
 ,
,
令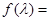 0,解得矩陣A的特征值
0,解得矩陣A的特征值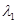 =
=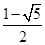 ,
,
 , 7分
, 7分
考點:矩陣的變換、特征矩陣、特征多項式、特征值.


 53隨堂測系列答案
53隨堂測系列答案科目:高中數學 來源: 題型:解答題
如圖所示,四邊形ABCD和四邊形AB′C′D分別是矩形和平行四邊形,其中各點的坐標分別為A(-1,2)、B(3,2)、C(3,-2)、D(-1,-2)、B′(3,7)、C′(3,3).求將四邊形ABCD變成四邊形AB′C′D的變換矩陣M.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com