
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 經過點
經過點![]() ,且離心率為
,且離心率為![]() .
.
(Ⅰ)求橢圓![]() 的方程;
的方程;
(Ⅱ)設![]() 是橢圓上的點,直線
是橢圓上的點,直線![]() 與
與![]() (
(![]() 為坐標原點)的斜率之積為
為坐標原點)的斜率之積為![]() .若動點
.若動點![]() 滿足
滿足![]() ,試探究是否存在兩個定點
,試探究是否存在兩個定點![]() ,使得
,使得![]() 為定值?若存在,求
為定值?若存在,求![]() 的坐標;若不存在,請說明理由.
的坐標;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】選修4-4:坐標系與參數方程
在平面直角坐標系中,曲線![]() 的方程為
的方程為![]() .以坐標原點為極點,
.以坐標原點為極點, ![]() 軸的非負半軸為極軸,建立極坐標系,曲線
軸的非負半軸為極軸,建立極坐標系,曲線![]() 的極坐標方程為
的極坐標方程為![]() .
.
(1)寫出曲線![]() 的參數方程和曲線
的參數方程和曲線![]() 的直角坐標方程;
的直角坐標方程;
(2)設點![]() 在曲線
在曲線![]() 上,點
上,點![]() 在曲線
在曲線![]() 上,求
上,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為了更好地規劃進貨的數量,保證蔬菜的新鮮程度,某蔬菜商店從某一年的銷售數據中,隨機抽取了8組數據作為研究對象,如下圖所示(![]() (噸)為買進蔬菜的質量,
(噸)為買進蔬菜的質量, ![]() (天)為銷售天數):
(天)為銷售天數):
| 2 | 3 | 4 | 5 | 6 | 7 | 9 | 12 |
| 1 | 2 | 3 | 3 | 4 | 5 | 6 | 8 |
(Ⅰ)根據上表數據在下列網格中繪制散點圖;

(Ⅱ)根據上表提供的數據,用最小二乘法求出![]() 關于
關于![]() 的線性回歸方程
的線性回歸方程![]() ;
;
(Ⅲ)根據(Ⅱ)中的計算結果,若該蔬菜商店準備一次性買進25噸,則預計需要銷售多少天.
參考公式:  ,
, ![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】2016年春節,“搶紅包”成為社會熱議的話題之一.某機構對春節期間用戶利用手機“搶紅包”的情況進行調查,如果一天內搶紅包的總次數超過10次為“關注點高”,否則為“關注點低”,調查情況如下表所示:

(1)填寫上表中x,y的值并判斷是否有95%以上的把握認為性別與關注點高低有關?
(2)現要從上述男性用戶中隨機選出3名參加一項活動,以X表示選中的同學中搶紅包總次數超過10次的人數,求隨機變量X的分布列及數學期望E(X).
下面的臨界值表供參考:

獨立性檢驗統計量 ,其中n=a+b+c+d.
,其中n=a+b+c+d.
查看答案和解析>>
科目:高中數學 來源: 題型:
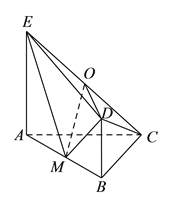
【題目】如圖,平面![]() 平面
平面![]() ,
,![]() 是等腰直角三角形,
是等腰直角三角形,![]() ,四邊形
,四邊形![]() 是直角梯形,
是直角梯形,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 分別為
分別為![]() ,
,![]() 的中點.
的中點.
(I)求證:![]() 平面
平面![]() .
.
(II)求直線![]() 和平面
和平面![]() 所成角的正弦值.
所成角的正弦值.
(III)能否在![]() 上找一點
上找一點![]() ,使得
,使得![]() 平面
平面![]() ?若能,請指出點
?若能,請指出點![]() 的位置,并加以證明;若不能,請說明理由.
的位置,并加以證明;若不能,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知△ABC是等腰三角形,AB=AC.
(1)特殊情形:如圖1,當DE∥BC時,有DBEC.(填“>”,“<”或“=”)
(2)發現探究:若將圖1中的△ADE繞點A順時針旋轉α(0°<α<180°)到圖2位置,則(1)中的結論還成立嗎?若成立,請給予證明;若不成立,請說明理由.
(3)拓展運用:如圖3,P是等腰直角三角形ABC內一點,∠ACB=90°,且PB=1,PC=2,PA=3,求∠BPC的度數.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com