
【題目】已知曲線C1: ![]() (t為參數)曲線C2:
(t為參數)曲線C2:![]() +y2=4.
+y2=4.
(1)在同一平面直角坐標系中,將曲線C2上的點按坐標變換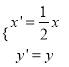 后得到曲線C′。求曲線C′的普通方程,并寫出它的參數方程;
后得到曲線C′。求曲線C′的普通方程,并寫出它的參數方程;
(2)若C1上的點P對應的參數為t=π/2,Q為C′上的動點,求PQ中點M到直線C3: ![]() (t為參數)的距離的最小值
(t為參數)的距離的最小值
【答案】(1)x2+y2=4, ![]() ;(2)
;(2)![]() .
.
【解析】試題分析:(1)直接根據坐標變換公式可得曲線C′的方程;(2) 曲線C′的方程的方程化為參數方程,根據參數方程可設M(-2+cosθ,2+sinθ),直線參數方程化為普通方程,利用點到直線的距離公式結合輔助角公式及三角函數的有界性可得結果.
試題解析:(1) 由 得到
得到![]() ①
①
將①代入![]() +y2=4,得
+y2=4,得![]() +y′2=4,即x′2+y′2=4.
+y′2=4,即x′2+y′2=4.
因此橢圓![]() +y2=4經伸縮變換后得到的曲線方程是x2+y2=4.
+y2=4經伸縮變換后得到的曲線方程是x2+y2=4.
它的參數方程為![]()
當t=π/2時,P(-4,4),Q(2cosθ,2sinθ),故M(-2+cosθ,2+sinθ)
曲線C3:為直線x-2y+8=0,
M到C3的距離d=![]() |(-2+cosθ)-2(2+sinθ)+8|=
|(-2+cosθ)-2(2+sinθ)+8|=![]() |cosθ-2sinθ+2|=
|cosθ-2sinθ+2|=![]() |
|![]() cos(θ+α)+2|
cos(θ+α)+2|
從而tanα=2時d的最小值為![]() |-
|-![]() +2|=
+2|=![]() .
.


 小學教材完全解讀系列答案
小學教材完全解讀系列答案科目:高中數學 來源: 題型:
【題目】已知(x,y)在映射f的作用下的像是(x+y,xy).
(1)求(-2,3)在f作用下的像;
(2)若在f作用下的像是(2,-3),求它的原像.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在極坐標系下,已知曲線C1:ρ=cosθ+sinθ和曲線C2:ρsin(θ-![]() )=
)=![]() .
.
(1)求曲線C1和曲線C2的直角坐標方程;
(2)當θ∈(0,π)時,求曲線C1和曲線C2公共點的一個極坐標.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】試求下列函數的定義域與值域:
(1)f(x)=(x-1)2+1,x∈{-1,0,1,2,3};
(2)f(x)=(x-1)2+1;
(3)f(x)=![]() ;
;
(4)f(x)=x-![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知冪函數f(x)=x![]() (m∈N*).
(m∈N*).
(1)試確定該函數的定義域,并指明該函數在其定義域上的單調性;
(2)若該函數還經過點(2, ![]() ),試確定m的值,并求滿足條件f(2-a)>f(a-1)的實數a的取值范圍.
),試確定m的值,并求滿足條件f(2-a)>f(a-1)的實數a的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
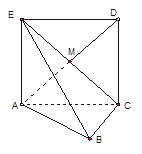
【題目】如圖,邊長為2的正方形ACDE所在的平面與平面ABC垂直,AD與CE的交點為M,![]() ,且AC=BC.
,且AC=BC.
(1)求證:![]() 平面EBC;
平面EBC;
(2)求二面角![]() 的大小.
的大小.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com