
【題目】在平面直角坐標系![]() 中,已知圓
中,已知圓![]() 經過拋物線
經過拋物線![]() 與坐標軸的三個交點.
與坐標軸的三個交點.
(1)求圓![]() 的方程;
的方程;
(2)經過點![]() 的直線
的直線![]() 與圓
與圓![]() 相交于
相交于![]() ,
,![]() 兩點,若圓
兩點,若圓![]() 在
在![]() ,
,![]() 兩點處的切線互相垂直,求直線
兩點處的切線互相垂直,求直線![]() 的方程.
的方程.
【答案】(1)![]() (2)
(2)![]() 和
和![]() .
.
【解析】
(1)方法一、求得拋物線與坐標軸的三個交點,設出圓的一般式方程,代入三點坐標,解方程組可得D,E,F,即可得到所求圓方程;方法二、由拋物線方程與圓的一般式方程,可令y=0,可得D,F,再由拋物線與y軸的交點,可得E,即可得到所求圓方程;
(2)求圓C的圓心和半徑,圓C在A,B兩點處的切線互相垂直,可得∠ACB![]() ,求得C到直線l的距離,討論直線l的斜率是否存在,由點到直線的距離公式,計算可得所求直線方程.
,求得C到直線l的距離,討論直線l的斜率是否存在,由點到直線的距離公式,計算可得所求直線方程.
(1)方法一:拋物線![]() 與坐標軸的三個交點坐標為
與坐標軸的三個交點坐標為![]() ,
,![]() ,
,![]() .
.
設圓![]() 的方程為
的方程為![]() ,
,
則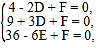 , 解得
, 解得 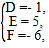
所以圓![]() 的方程為
的方程為![]() .
.
方法二:設圓![]() 的方程為
的方程為![]() .
.
令![]() ,得
,得![]() .
.
因為圓![]() 經過拋物線
經過拋物線![]() 與
與![]() 軸的交點,
軸的交點,
所以![]() 與方程
與方程![]() 同解,
同解,
所以![]() ,
,![]() .
.
因此圓![]() .
.
因為拋物線![]() 與
與![]() 軸的交點坐標為
軸的交點坐標為![]() ,
,
又所以點![]() 也在圓
也在圓![]() 上,所以
上,所以![]() ,解得
,解得![]() .
.
所以圓![]() 的方程為
的方程為![]() .
.
(2)由(1)可得,圓:![]() ,
,
故圓心![]() ,半徑
,半徑![]() .
.
因為圓![]() 在
在![]() ,
,![]() 兩點處的切線互相垂直,所以
兩點處的切線互相垂直,所以![]() .
.
所以![]() 到直線
到直線![]() 的距離
的距離![]() .
.
① 當直線![]() 的斜率不存在時,
的斜率不存在時,![]() ,符合題意;
,符合題意;
② 當直線![]() 的斜率存在時,設
的斜率存在時,設![]() ,即
,即![]() ,
,
所以![]() ,解得
,解得![]() ,
,
所以直線![]() ,即
,即![]() .
.
綜上,所求直線![]() 的方程為
的方程為![]() 和
和![]() .
.
方法三:①當直線![]() 的斜率存在時,設直線
的斜率存在時,設直線![]() 的方程為
的方程為![]() ,
,
![]() ,
,![]() ,將直線
,將直線![]() 的方程代入圓
的方程代入圓![]() 的方程得:
的方程得:
![]() ,
,
即![]()
![]() ,
,![]() .
.
因為圓![]() 在點
在點![]() ,
,![]() 兩點處的切線互相垂直,所以
兩點處的切線互相垂直,所以![]() ,
,
所以![]() ,即
,即![]() ,
,
所以![]() ,
,
即![]() ,
,
即![]() ,
,
![]() ,
,
即![]() ,解得
,解得![]() ,所以直線
,所以直線![]() :
:![]() ,
,
即![]() .
.
②當直線![]() 的斜率不存在時,
的斜率不存在時,![]() :
:![]() ,符合題意;
,符合題意;
綜上,所求直線![]() 的方程為
的方程為![]() 和
和![]() .
.


科目:高中數學 來源: 題型:
【題目】某企業常年生產一種出口產品,根據預測可知,進入21世紀以來,該產品的產量平穩增長.記2009年為第1年,且前4年中,第x年與年產量f(x) 萬件之間的關系如下表所示:
x | 1 | 2 | 3 | 4 |
f(x) | 4.00 | 5.58 | 7.00 | 8.44 |
若f(x)近似符合以下三種函數模型之一:f(x)=ax+b,f(x)=2x+a,f(x)=log![]() x+a.
x+a.
(1)找出你認為最適合的函數模型,并說明理由,然后選取其中你認為最適合的數據求出相應的解析式;
(2)因遭受某國對該產品進行反傾銷的影響,2015年的年產量比預計減少30%,試根據所建立的函數模型,確定2015年的年產量.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設橢圓C: ![]() ,定義橢圓C的“相關圓”方程為
,定義橢圓C的“相關圓”方程為![]() ,若拋物線
,若拋物線![]() 的焦點與橢圓C的一個焦點重合,且橢圓C短軸的一個端點和其兩個焦點構成直角三角形。
的焦點與橢圓C的一個焦點重合,且橢圓C短軸的一個端點和其兩個焦點構成直角三角形。
(I)求橢圓C的方程和“相關圓”E的方程;
(II)過“相關圓”E上任意一點P作“相關圓”E的切線l與橢圓C交于A,B兩點,O為坐標原點。
(i)證明∠AOB為定值;
(ii)連接PO并延長交“相關圓”E于點Q,求△ABQ面積的取值范圍。
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,是一個半圓柱與多面體![]() 構成的幾何體,平面
構成的幾何體,平面![]() 與半圓柱的下底面共面,且
與半圓柱的下底面共面,且![]() ,
, ![]() 為弧
為弧![]() 上(不與
上(不與![]() 重合)的動點.
重合)的動點.
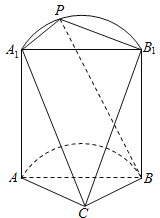
(1)證明: ![]() 平面
平面![]() ;
;
(2)若四邊形![]() 為正方形,且
為正方形,且![]() ,
, ![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,從一個面積為![]() 的半圓形鐵皮上截取兩個高度均為
的半圓形鐵皮上截取兩個高度均為![]() 的矩形,并將截得的兩塊矩形鐵皮分別以
的矩形,并將截得的兩塊矩形鐵皮分別以![]() ,
,![]() 為母線卷成兩個高均為
為母線卷成兩個高均為![]() 的圓柱(無底面,連接部分材料損失忽略不計).記這兩個圓柱的體積之和為
的圓柱(無底面,連接部分材料損失忽略不計).記這兩個圓柱的體積之和為![]() .
.

(1)將![]() 表示成
表示成![]() 的函數關系式,并寫出
的函數關系式,并寫出![]() 的取值范圍;
的取值范圍;
(2)求兩個圓柱體積之和![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖四棱錐![]() 中,
中, ![]() 是梯形,AB∥CD,
是梯形,AB∥CD, ![]() ,AB=PD=4,CD=2,
,AB=PD=4,CD=2, ![]() ,M為CD的中點,N為PB上一點,且
,M為CD的中點,N為PB上一點,且![]() .
.
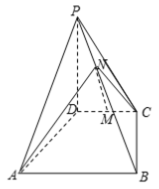
(1)若![]() MN∥平面PAD;
MN∥平面PAD;
(2)若直線AN與平面PBC所成角的正弦值為![]() ,求異面直線AD與直線CN所成角的余弦值。
,求異面直線AD與直線CN所成角的余弦值。
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com