
【題目】用數(shù)字![]() 組成沒有重復數(shù)字的四位數(shù).
組成沒有重復數(shù)字的四位數(shù).
(Ⅰ)可組成多少個不同的四位數(shù)?
(Ⅱ)可組成多少個不同的四位偶數(shù)?
(Ⅲ)將(Ⅰ)中的四位數(shù)按從小到大的順序排成一數(shù)列,問第![]() 項是什么?
項是什么?
【答案】(Ⅰ)300;(Ⅱ)156;(Ⅲ)2301
【解析】
試題分析:(Ⅰ)根據(jù)排列性質(zhì),先排最高為千位,不能排0,所以可以從1,2,3,4,5中任意取一個排在最高位,有![]() 種排法,然后排剩余的三個位置,可以從0和剩余的4個數(shù)字這5個數(shù)字中,任意取3個排在剩余的3個位置,共有
種排法,然后排剩余的三個位置,可以從0和剩余的4個數(shù)字這5個數(shù)字中,任意取3個排在剩余的3個位置,共有![]() 種排法,根據(jù)乘法原理,完成這件事共有:
種排法,根據(jù)乘法原理,完成這件事共有:![]() 種;(Ⅱ)組成4位偶數(shù),末位只能排0或2或4,末位排0時,其他位置任意排,有
種;(Ⅱ)組成4位偶數(shù),末位只能排0或2或4,末位排0時,其他位置任意排,有![]() 種排法,末位排2或4時,最高位不能排0,此時有
種排法,末位排2或4時,最高位不能排0,此時有![]() 種,再根據(jù)加法原理,完成這件事共有
種,再根據(jù)加法原理,完成這件事共有![]() +
+![]() 種方法;(Ⅲ)將(Ⅰ)中的數(shù)從小到大排列,最高位為1時,有
種方法;(Ⅲ)將(Ⅰ)中的數(shù)從小到大排列,最高位為1時,有![]() 個,同理最高位為2時也有
個,同理最高位為2時也有![]() 個,第85個數(shù)應該是首位為2的時候,前兩個數(shù)字為20時,有
個,第85個數(shù)應該是首位為2的時候,前兩個數(shù)字為20時,有![]() 個,前兩個數(shù)字為21時,有
個,前兩個數(shù)字為21時,有![]() 個,此時共84個數(shù),所以第85個數(shù)為2301.
個,此時共84個數(shù),所以第85個數(shù)為2301.
試題解析:(Ⅰ)共![]() 個
個
(Ⅱ)分為兩類:0在末位,則有![]() 個:0不在末位,則有
個:0不在末位,則有![]() 個.∴共60+96=156個.
個.∴共60+96=156個.
(Ⅲ)首位為1的有60個;前兩位為20的有12個;
前兩位為21的有12個;
因而第85項是前兩位為23的最小數(shù),即為2301


科目:高中數(shù)學 來源: 題型:
【題目】已知圓心為C的圓:(x﹣a)2+(y﹣b)2=8(a,b為正整數(shù))過點A(0,1),且與直線y﹣3﹣2 ![]() =0相切.
=0相切.
(1)求圓C的方程;
(2)若過點M(4,﹣1)的直線l與圓C相交于E,F(xiàn)兩點,且 ![]() =0.求直線l的方程.
=0.求直線l的方程.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
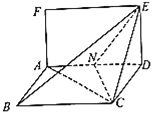
【題目】已知矩形![]() 和菱形
和菱形![]() 所在平面互相垂直,如圖,其中
所在平面互相垂直,如圖,其中![]() ,
, ![]() ,
, ![]() ,點
,點![]() 為線段
為線段![]() 的中點.
的中點.
(Ⅰ)試問在線段![]() 上是否存在點
上是否存在點![]() ,使得直線
,使得直線![]() 平面
平面![]() ?若存在,請證明
?若存在,請證明![]() 平面
平面![]() ,并求出
,并求出![]() 的值,若不存在,請說明理由;
的值,若不存在,請說明理由;
(Ⅱ)求二面角![]() 的正弦值.
的正弦值.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】在平面直角坐標系中,O為坐標原點,A、B、C三點滿足 ![]() =
= ![]() +
+ ![]()
![]() .
.
(1)求證:A、B、C三點共線;
(2)求 ![]() 的值;
的值;
(3)已知A(1,cosx)、B(1+cosx,cosx),x∈[0, ![]() ],f(x)=
],f(x)= ![]()
![]() ﹣(2m+
﹣(2m+ ![]() )|
)| ![]() |的最小值為﹣
|的最小值為﹣ ![]() ,求實數(shù)m的值.
,求實數(shù)m的值.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】為了響應教育部頒布的《關(guān)于推進中小學生研學旅行的意見》,某校計劃開設八門研學旅行課程,并對全校學生的選課意向進行調(diào)查(調(diào)查要求全員參與,每個學生必須從八門課程中選出唯一一門課程).本次調(diào)查結(jié)果如下.
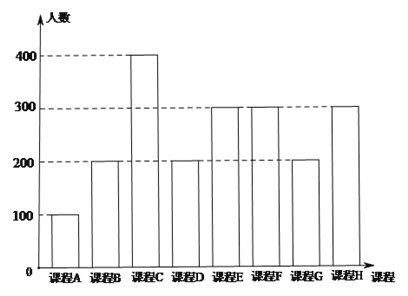
圖中,課程![]() 為人文類課程,課程
為人文類課程,課程![]() 為自然科學類課程.為進一步研究學生選課意向,結(jié)合上面圖表,采取分層抽樣方法從全校抽取1%的學生作為研究樣本組(以下簡稱“組
為自然科學類課程.為進一步研究學生選課意向,結(jié)合上面圖表,采取分層抽樣方法從全校抽取1%的學生作為研究樣本組(以下簡稱“組![]() ”).
”).
(Ⅰ)在“組![]() ”中,選擇人文類課程和自然科學類課程的人數(shù)各有多少?
”中,選擇人文類課程和自然科學類課程的人數(shù)各有多少?
(Ⅱ)某地舉辦自然科學營活動,學校要求:參加活動的學生只能是“組![]() ”中選擇
”中選擇![]() 課
課
程或![]() 課程的同學,并且這些同學以自愿報名繳費的方式參加活動. 選擇
課程的同學,并且這些同學以自愿報名繳費的方式參加活動. 選擇![]() 課程的學生中有
課程的學生中有![]() 人參加科學營活動,每人需繳納
人參加科學營活動,每人需繳納![]() 元,選擇
元,選擇![]() 課程的學生中有
課程的學生中有![]() 人參加該活動,每人需繳納
人參加該活動,每人需繳納![]() 元.記選擇
元.記選擇![]() 課程和
課程和![]() 課程的學生自愿報名人數(shù)的情況為
課程的學生自愿報名人數(shù)的情況為![]() ,參加活動的學生繳納費用總和為
,參加活動的學生繳納費用總和為![]() 元.
元.
①當![]() 時,寫出
時,寫出![]() 的所有可能取值;
的所有可能取值;
②若選擇![]() 課程的同學都參加科學營活動,求
課程的同學都參加科學營活動,求![]() 元的概率.
元的概率.
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com