已知函數
．
（1）若
在
上存在零點，求實數
的取值范圍；
（2）當
時，若對任意的
，總存在
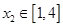使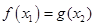
成立，求實數
的取值范圍．
科目：高中數學 來源： 題型：解答題
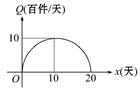
某食品公司為了解某種新品種食品的市場需求,進行了20天的測試,人為地調控每天產品的單價P(元/件)：前10天每天單價呈直線下降趨勢(第10天免費贈送品嘗),后10天呈直線上升,其中4天的單價記錄如表：
| 時間(將第x天記為x)x | 1 | 10 | 11 | 18 |
| 單價(元/件)P | 9 | 0 | 1 | 8 |
查看答案和解析>>
科目：高中數學 來源： 題型：解答題
提高過江大橋的車輛通行能力可改善整個城市的交通狀況．在一般情況下，大橋上的車流速度
（單位：千米/小時）是車流密度
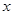（單位：輛/千米）的函數．當橋上的車流密度達到200輛/千米時，造成堵塞，此時車流速度為0；當車流密度不超過20輛/千米時，車流速度為60千米/小時．研究表明：當
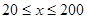時，車流速度是車流密度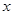的一次函數．
（1）當
時，求函數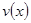
的表達式；
（2）當車流密度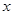為多大時，車流量（單位時間內通過橋上某觀測點的車輛數，單位：輛/小時）
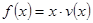可以達到最大，并求出最大值．（精確到1輛/小時）
查看答案和解析>>
科目：高中數學 來源： 題型：解答題
為了保護環境，某工廠在國家的號召下，把廢棄物回收轉化為某種產品，經測算，處理成本
（萬元）與處理量
（噸）之間的函數關系可近似的表示為：
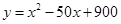，且每處理一噸廢棄物可得價值為
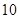萬元的某種產品，同時獲得國家補貼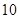萬元．
（1）當
時，判斷該項舉措能否獲利？如果能獲利，求出最大利潤；
如果不能獲利，請求出國家最少補貼多少萬元，該工廠才不會虧損？
（2）當處理量為多少噸時，每噸的平均處理成本最少？
查看答案和解析>>
科目：高中數學 來源： 題型：解答題
如圖所示，為了制作一個圓柱形燈籠，先要制作4個全等的矩形骨架，總計耗用9.6米鐵絲，再用S平方米塑料片制成圓柱的側面和下底面(不安裝上底面)．當圓柱底面半徑r取何值時，S取得最大值？并求出該最大值(結果精確到0.01平方米)．
查看答案和解析>>
科目：高中數學 來源： 題型：解答題
已知函數f(x)＝
在區間[－1，1]上是增函數．
(1)求實數a的值組成的集合A；
(2)設x1、x2是關于x的方程f(x)＝
的兩個相異實根，若對任意a∈A及t∈[－1，1]，不等式m2＋tm＋1≥|x1－x2|恒成立，求實數m的取值范圍．
查看答案和解析>>
科目：高中數學 來源： 題型：解答題
我國遼東半島普蘭附近的泥炭層中，發掘出的古蓮子，至今大部分還能發芽開花，這些古蓮子是多少年以前的遺物呢？要測定古物的年代，可用放射性碳法．在動植物的體內都含有微量的放射性14C，動植物死亡后，停止了新陳代謝，14C不再產生，且原有的14C會自動衰變，經過5570年(叫做14C的半衰期)，它的殘余量只有原始量的一半，經過科學家測定知道，若14C的原始含量為a，則經過t年后的殘余量a′(與a之間滿足a′＝a·e－kt)．現測得出土的古蓮子中14C殘余量占原量的87.9%，試推算古蓮子的生活年代．
查看答案和解析>>
科目：高中數學 來源： 題型：解答題
某廠生產某種產品的年固定成本為250萬元,每生產x千件,需另投入成本為C(x),當年產量不足80千件時,C(x)=
x2+10x(萬元).當年產量不小于80千件時,C(x)=51x+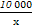
-1450(萬元).每件商品售價為0.05萬元.通過市場分析,該廠生產的商品能全部售完.
(1)寫出年利潤L(x)(萬元)關于年產量x(千件)的函數解析式.
(2)年產量為多少千件時,該廠在這一商品的生產中所獲利潤最大?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
；（2）
．
上存在零點，只需
即可；
的值域的子集即可．
的對稱軸為
，所以
即
解得
．
的值域的子集
， 
的值域：
時，
為常函數，不符合題意；
，
，∴
解得
；
，
，∴
解得
．
×
0＋80.25×
＋(
×
)6－
；
；