
若數(shù)列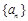 滿足
滿足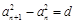 ,其中
,其中 為常數(shù),則稱數(shù)列
為常數(shù),則稱數(shù)列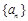 為等方差數(shù)列
為等方差數(shù)列
已知等方差數(shù)列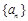 滿足
滿足 。
。
(Ⅰ)求數(shù)列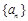 的通項公式;
的通項公式;
(Ⅱ)記 ,則當實數(shù)
,則當實數(shù)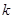 大于4時,不等式
大于4時,不等式 能否對于一切的
能否對于一切的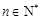 恒成立?請說明理由
恒成立?請說明理由
(Ⅰ)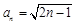 ;
;
(Ⅱ)當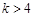 時,不等式
時,不等式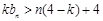 對于一切的
對于一切的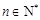 恒成立.
恒成立.
【解析】本試題主要考查了等方差數(shù)列的定義的理解和運用,涉及到求解數(shù)列的通項公式和數(shù)列解決不等式的恒成立問題的綜合運用。
(1)根據(jù)數(shù)列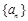 滿足
滿足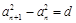 ,其中
,其中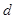 為常數(shù),則稱數(shù)列
為常數(shù),則稱數(shù)列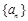 為等方差數(shù)列和
為等方差數(shù)列和 ,得到公差d,進而求解通項公式。
,得到公差d,進而求解通項公式。
(2)因為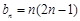 ,不等式
,不等式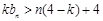 恒成立,
恒成立,
即 對于一切的
對于一切的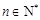 恒成立,運用分離參數(shù)法的思想得到證明。
恒成立,運用分離參數(shù)法的思想得到證明。
解:(Ⅰ)由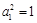 ,
,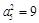 得,
得,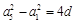 ,
,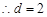 .…………………3分
.…………………3分
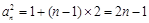 ,
,
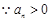 ,
,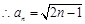 ,
,
數(shù)列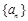 的通項公式為
的通項公式為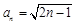 ;………………… 6分
;………………… 6分
(Ⅱ)解法一: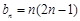 ,不等式
,不等式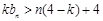 恒成立,
恒成立,
即 對于一切的
對于一切的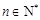 恒成立.
………………… 8分
恒成立.
………………… 8分
設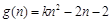 .
………………… 9分
.
………………… 9分
當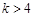 時,由于對稱軸
時,由于對稱軸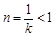 ,且
,且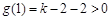
而函數(shù)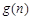 在
在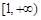 是增函數(shù),………………… 10分
是增函數(shù),………………… 10分
不等式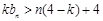 恒成立,
恒成立,
即當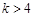 時,不等式
時,不等式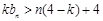 對于一切的
對于一切的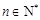 恒成立.
……………… 12分
恒成立.
……………… 12分
解法二: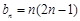 ,不等式
,不等式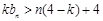 恒成立,
恒成立,
即 對于一切的
對于一切的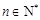 恒成立.
………………… 8分
恒成立.
………………… 8分
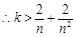 ………………… 9分
………………… 9分
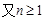 ,
,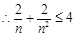 .………………… 10分
.………………… 10分
而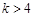
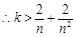 恒成立.
恒成立.
故當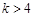 時,不等式
時,不等式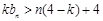 對于一切的
對于一切的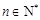 恒成立.
………………… 12分
恒成立.
………………… 12分


科目:高中數(shù)學 來源: 題型:
| an+2 |
| an+1 |
| an+1 |
| an |
| 3 |
| 2 |
| 3nan-1 |
| 2an-1+n-1 |
| n•3n |
| 3n-1 |
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
| π |
| 2 |
| 1 |
| sina |
| 3 |
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
| 4an-2 |
| an+1 |
| 146 |
| 65 |
查看答案和解析>>
科目:高中數(shù)學 來源:2012-2013學年四川省成都外國語學校高三(上)11月月考數(shù)學試卷(解析版) 題型:填空題
 (λ為常數(shù)),則稱數(shù)列{an}為比等差數(shù)列,λ稱為比公差.現(xiàn)給出以下命題,其中所有真命題的序號是 .
(λ為常數(shù)),則稱數(shù)列{an}為比等差數(shù)列,λ稱為比公差.現(xiàn)給出以下命題,其中所有真命題的序號是 . ,則數(shù)列{an}是比等差數(shù)列,且比公差λ=2;
,則數(shù)列{an}是比等差數(shù)列,且比公差λ=2; ,a1=2,則此數(shù)列的通項為
,a1=2,則此數(shù)列的通項為 -1,且{an}不是比等差數(shù)列;
-1,且{an}不是比等差數(shù)列; ,且an=
,且an= ,則此數(shù)列的通項為an=
,則此數(shù)列的通項為an= ,且{an}不是比等差數(shù)列.
,且{an}不是比等差數(shù)列.查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com