
【題目】如圖所示,矩形![]() 中,
中,![]() ,
,![]() 平面
平面![]() ,
,![]() ,
,![]() 為
為![]() 上的點,且
上的點,且![]() 平面
平面![]() .
.
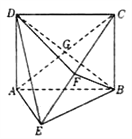
(1)求證:![]() 平面
平面![]() ;
;
(2)求平面![]() 與平面
與平面![]() 所成角的余弦值.
所成角的余弦值.
【答案】(1)見解析;(2)![]() .
.
【解析】試題分析:(1)由![]() 面
面![]() ,可得
,可得![]() ,所以
,所以![]() ,由
,由![]() 面
面![]() ,可得
,可得![]() .
.
由線面垂直的判定定理可得![]() 平面
平面![]() ;(2)以
;(2)以![]() 為原點,
為原點,![]() 所在直線為
所在直線為![]() 軸,
軸,![]() 所在直線為
所在直線為![]() 軸,過
軸,過![]() 且垂直于平面
且垂直于平面![]() 的直線為
的直線為![]() 軸建立空間直角坐標系,分別根據向量垂直數量積為零列方程組求出平面
軸建立空間直角坐標系,分別根據向量垂直數量積為零列方程組求出平面![]() 與平面
與平面![]() 的一個法向量,根據空間向量夾角余弦公式,可得平面
的一個法向量,根據空間向量夾角余弦公式,可得平面![]() 與平面
與平面![]() 所成角的余弦值.
所成角的余弦值.
試題解析:(1)因為![]() 面
面![]() ,所以
,所以![]() ,
,
又![]() ,所以
,所以![]() .
.
因為![]() 面
面![]() ,所以
,所以![]() .
.
又![]() ,所以
,所以![]() 面
面![]() ,即
,即![]() 平面
平面![]() .
.

(2)以![]() 為原點,
為原點,![]() 所在直線為
所在直線為![]() 軸,
軸,![]() 所在直線為
所在直線為![]() 軸,過
軸,過![]() 且垂直于平面
且垂直于平面![]() 的直線為
的直線為![]() 軸建立空間直角坐標系,則相關點的坐標為
軸建立空間直角坐標系,則相關點的坐標為![]() ,
,![]() ,
,![]() ,
,![]() ,
,
設平面![]() 的法向量
的法向量![]() ,平面
,平面![]() 的法向量為
的法向量為![]() ,易知
,易知![]() ,
,
令![]() ,則
,則 ,故
,故![]() ,令
,令![]() ,得
,得 ,
,![]() ,
,
于是,![]()

![]() .
.
此即平面![]() 與平面
與平面![]() 所成角的余弦值.
所成角的余弦值.


科目:高中數學 來源: 題型:
【題目】選修4-4:坐標系與參數方程
已知曲線![]() 的參數方程為
的參數方程為![]() (
(![]() 為參數),以平面直角坐標系的原點為極點,
為參數),以平面直角坐標系的原點為極點,![]() 軸的正半軸為極軸建立極坐標系.
軸的正半軸為極軸建立極坐標系.
(1)求曲線![]() 的普通方程,并說明其表示什么軌跡;
的普通方程,并說明其表示什么軌跡;
(2)若直線![]() 的極坐標方程為
的極坐標方程為![]() ,試判斷直線
,試判斷直線![]() 與曲線
與曲線![]() 的位置關系,若相交,請求出其弦長.
的位置關系,若相交,請求出其弦長.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() :
:![]()
![]() 的左焦點為
的左焦點為![]() ,上頂點為
,上頂點為![]() ,長軸長為
,長軸長為![]() ,
,![]() 為直線
為直線![]() :
:![]() 上的動點,
上的動點,![]() ,
,![]() .當
.當![]() 時,
時,![]() 與
與![]() 重合.
重合.
(1)若橢圓![]() 的方程;
的方程;
(2)若直線![]() 交橢圓
交橢圓![]() 于
于![]() ,
,![]() 兩點,若
兩點,若![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
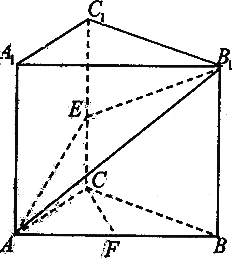
【題目】如圖,直三棱柱![]() 中,
中,![]() 且
且![]() ,
,![]() 是棱
是棱![]() 上的動點,
上的動點,![]() 是
是![]() 的中點.
的中點.
(1)當![]() 是
是![]() 中點時,求證:
中點時,求證:![]() 平面
平面![]() ;
;
(2)在棱![]() 上是否存在點
上是否存在點![]() ,使得平面
,使得平面![]() 與平面
與平面![]() 所成銳二面角為
所成銳二面角為![]() ,若存在,求
,若存在,求![]() 的長,若不存在,請說明理由.
的長,若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
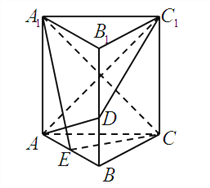
【題目】如圖,正三棱柱![]() 的所有棱長均
的所有棱長均![]() ,
,![]() 為棱
為棱![]() (不包括端點)上一動點,
(不包括端點)上一動點,![]() 是
是![]() 的中點.
的中點.
(Ⅰ)若![]() ,求
,求![]() 的長;
的長;
(Ⅱ)當![]() 在棱
在棱![]() (不包括端點)上運動時,求平面
(不包括端點)上運動時,求平面![]() 與平面
與平面![]() 的夾角的余弦值的取值范圍.
的夾角的余弦值的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】[選修4-4:坐標系與參數方程]
在直角坐標系![]() 中,以坐標原點為極點,
中,以坐標原點為極點,![]() 軸正半軸為極軸建立極坐標系.已知直線
軸正半軸為極軸建立極坐標系.已知直線![]() 的參數方程是
的參數方程是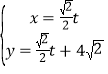 (
(![]() 是參數),圓
是參數),圓![]() 的極坐標方程為
的極坐標方程為![]() .
.
(1)求圓心![]() 的直角坐標;
的直角坐標;
(2)由直線![]() 上的點向圓
上的點向圓![]() 引切線,并切線長的最小值.
引切線,并切線長的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
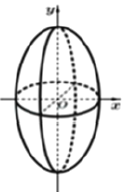
【題目】祖暅是我國齊梁時代的數學家,是祖沖之的兒子,他提出了一條原理:“冪勢既同,則積不容易.”這里的“冪”指水平截面的面積.“勢”指高,這句話的意思是:兩個等高的幾何體若在所有等高處的水平截面的面積相等,則這兩個幾何體體積相等。于是可把半徑相等的半球(底面在下)和圓柱(圓柱高等于半徑)放在同一水平面上,圓柱里再放一個半徑和高都與圓柱相等的圓錐(錐尖朝下),考察圓柱里被圓錐截剩的立體,這樣在同一高度用平行平面截得的半球截面和圓柱中剩余立體截得的截面面積相等,因此半球的體積等于圓柱中剩余立體的體積.設由橢圓![]() 所圍成的平面圖形繞
所圍成的平面圖形繞![]() 軸旋轉一周后,得一橄欖狀的幾何體(如圖,稱為“橢球體”),請類比以上所介紹的應用祖暅原理求球體體積的做法求這個橢球體的體積.其體積等于________.
軸旋轉一周后,得一橄欖狀的幾何體(如圖,稱為“橢球體”),請類比以上所介紹的應用祖暅原理求球體體積的做法求這個橢球體的體積.其體積等于________.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com