
【題目】已知函數![]() .
.
(1)討論函數![]() 的單調區間;
的單調區間;
(2)若![]() ,
, ![]() 恒成立,求
恒成立,求![]() 的取值范圍.
的取值范圍.
【答案】(1)![]() (2)
(2)![]()
【解析】試題分析:(1) 求出函數的導數,通過討論![]() 的范圍,
的范圍, ![]() 得增區間,
得增區間, ![]() 得減區間; (2)問題轉化為
得減區間; (2)問題轉化為![]() ,討論
,討論![]() 的范圍,根據函數的單調性求出
的范圍,根據函數的單調性求出![]() 的最小值即可求出
的最小值即可求出![]() 的范圍.
的范圍.
試題解析:(1)![]() .
.
(i)當![]() 時,
時, ![]() ,函數
,函數![]() 在
在![]() 上單調遞增;
上單調遞增;
(ii)當![]() 時,令
時,令![]() ,則
,則![]() ,
,
當![]() ,即
,即![]() ,函數
,函數![]() 單調遞增;
單調遞增;
當![]() ,即
,即![]() 時,函數
時,函數![]() 單調遞減.
單調遞減.
綜上,當![]() 時,函數
時,函數![]() 在
在![]() 上單調遞增;當
上單調遞增;當![]() 時,函數
時,函數![]() 的單調遞增區間是
的單調遞增區間是![]() ,單調遞減區間是
,單調遞減區間是![]() .
.
(2)令![]() ,由(1)可知,函數
,由(1)可知,函數![]() 的最小值為
的最小值為![]() ,所以
,所以![]() ,即
,即![]() .
.
![]() 恒成立與
恒成立與![]() 恒成立等價,
恒成立等價,
令![]() ,即
,即![]() ,則
,則![]() .
.
①當![]() 時,
時, ![]() .(或令
.(或令![]() ,則
,則
![]() 在
在![]() 上遞增,∴
上遞增,∴![]() ,∴
,∴![]() 在
在![]() 上遞增,∴
上遞增,∴![]() .
.
∴![]() ).
).
∴![]() 在區間
在區間![]() 上單調遞增,
上單調遞增,
∴![]() ,
,
∴![]() 恒成立.
恒成立.
②當![]() 時,令
時,令![]() ,則
,則![]() ,
,
當![]() 時,
時, ![]() ,函數
,函數![]() 單調遞增.
單調遞增.
又![]() ,
, ![]() ,
,
∴存在![]() ,使得
,使得![]() ,故當
,故當![]() 時,
時, ![]() ,即
,即![]() ,故函數
,故函數![]() 在
在![]() 上單調遞減;當
上單調遞減;當![]() 時,
時, ![]() ,即
,即![]() ,故函數
,故函數![]() 在
在![]() 上單調遞增,
上單調遞增,
∴![]() ,
,
即![]() ,
, ![]() 不恒成立,
不恒成立,
綜上所述, ![]() 的取值范圍是
的取值范圍是![]() .
.


科目:高中數學 來源: 題型:
【題目】如圖所示,已知圓![]() 的圓心在直線
的圓心在直線![]() 上,且該圓存在兩點關于直線
上,且該圓存在兩點關于直線![]() 對稱,又圓
對稱,又圓![]() 與直線
與直線![]() 相切,過點
相切,過點![]() 的動直線
的動直線![]() 與圓
與圓![]() 相交于
相交于![]() 兩點,
兩點,![]() 是
是![]() 的中點,直線
的中點,直線![]() 與
與![]() 相交于點
相交于點![]() .
.
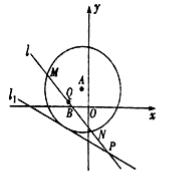
(1)求圓![]() 的方程;
的方程;
(2)當![]() 時,求直線
時,求直線![]() 的方程;
的方程;
(3)![]() 是否為定值?如果是,求出其定值;如果不是,請說明理由.
是否為定值?如果是,求出其定值;如果不是,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
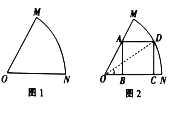
【題目】某車間為了制作某個零件,需從一塊扇形的鋼板余料(如圖1)中按照圖2的方式裁剪一塊矩形鋼板![]() ,其中頂點
,其中頂點![]() 、
、![]() 在半徑
在半徑![]() 上,頂點
上,頂點![]() 在半徑
在半徑![]() 上,頂點
上,頂點![]() 在
在![]() 上,
上, ![]() ,
, ![]() .設
.設![]() ,矩形
,矩形![]() 的面積為
的面積為![]() .
.
(1)用含![]() 的式子表示
的式子表示![]() ,
, ![]() 的長;
的長;
(2)試將![]() 表示為
表示為![]() 的函數;
的函數;
(3)求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知圓![]() 滿足:①圓心在第一象限,截
滿足:①圓心在第一象限,截![]() 軸所得弦長為2;②被
軸所得弦長為2;②被![]() 軸分成兩段圓弧,其弧長的比為
軸分成兩段圓弧,其弧長的比為![]() ;③圓心到直線
;③圓心到直線![]() 的距離為
的距離為![]() .
.
(Ⅰ)求圓![]() 的方程;
的方程;
(Ⅱ)若點![]() 是直線
是直線![]() 上的動點,過點
上的動點,過點![]() 分別做圓
分別做圓![]() 的兩條切線,切點分別為
的兩條切線,切點分別為![]() ,
, ![]() ,求證:直線
,求證:直線![]() 過定點.
過定點.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】對于函數![]() ,若在定義域內存在實數
,若在定義域內存在實數![]() ,滿足
,滿足![]() ,則稱
,則稱![]() 為“局部奇函數”.
為“局部奇函數”.
![]() 為定義在
為定義在![]() 上的“局部奇函數”;
上的“局部奇函數”;
![]() 曲線
曲線![]() 與
與![]() 軸交于不同的兩點;
軸交于不同的兩點;
若![]() 為假命題,
為假命題, ![]() 為真命題,求
為真命題,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】一個盒子中裝有5張編號依次為1、2、3、4、5的卡片,這5 張卡片除號碼外完全相同.現進行有放回的連續抽取2 次,每次任意地取出一張卡片.
(1)求出所有可能結果數,并列出所有可能結果;
(2)求事件“取出卡片號碼之和不小于7 或小于5”的概率.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com