【題目】近年來，空氣質量成為人們越來越關注的話題，空氣質量指數（
，簡稱
）是定量描述空氣質量狀況的指數，空氣質量按照
大小分為六級， 
為優； 
為良； 
為輕度污染； 
為中度污染； 
為重度污染；大于300為嚴重污染．環保部門記錄了2017年某月哈爾濱市10天的
的莖葉圖如下：
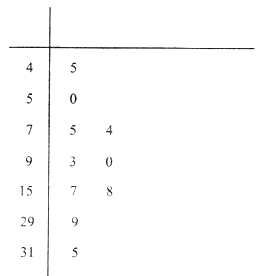
（1）利用該樣本估計該地本月空氣質量優良（
）的天數；（按這個月總共30天計算）
（2）現工作人員從這10天中空氣質量為優良的日子里隨機抽取2天進行某項研究，求抽取的2天中至少有一天空氣質量是優的概率；
（3）將頻率視為概率，從本月中隨機抽取3天，記空氣質量優良的天數為
，求
的概率分布列和數學期望.
科目：高中數學 來源： 題型：
【題目】已知函數y=f（x）是定義域為R的偶函數，當x≥0時，f（x）=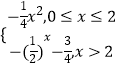 
，若關于x的方程[f（x）]2+af（x）+ 
=0，a∈R有且僅有8個不同實數根，則實數a的取值范圍是
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】一家公司計劃生產某種小型產品的月固定成本為1萬元，每生產1萬件需要再投入2萬元，設該公司一個月內生產該小型產品x萬件并全部銷售完，每萬件的銷售收入為4﹣x萬元，且每萬件國家給予補助2e﹣ 
﹣ 
萬元．（e為自然對數的底數，e是一個常數）
（1）寫出月利潤f（x）（萬元）關于月產量x（萬件）的函數解析式
（2）當月產量在[1，2e]萬件時，求該公司在生產這種小型產品中所獲得的月利潤最大值（萬元）及此時的月生成量值（萬件）．（注：月利潤=月銷售收入+月國家補助﹣月總成本）
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數f（x）=x3+（1﹣a） x2﹣a（a+2）x+b（a，b∈R）．
（1）若函數f（x）的圖象過原點，且在原點處的切線斜率是﹣3，求a，b的值；
（2）若函數f（x）在區間（﹣1，1）上不單調，求a的取值范圍．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】設函數f（x）=x2﹣2tx+2，其中 t∈R．
（1）若t=1，求函數f（x）在區間[0，4]上的取值范圍；
（2）若t=1，且對任意的x∈[a，a+2]，都有f（x）＜5，求實數a的取值范圍；
（3）若對任意的x1 ， x2∈[0，4]，都有f（x1）﹣f（x2）≤8，求t的取值范圍．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某旅游景區的景點A處和B處之間有兩種到達方式，一種是沿直線步行，另一種是沿索道乘坐纜車，現有一名游客從A處出發，以50m/min的速度勻速步行，30min后到達B處，在B處停留20min后，再乘坐纜車回到A處．假設纜車勻速直線運動的速度為150m/mm．
（1）求該游客離景點A的距離y（m）關于出發后的時間x（mm）的函數解析式，并指出該函數的定義域；
（2）做出（1）中函數的圖象，并求該游客離景點A的距離不小于1000m的總時長． 
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知 a∈R，函數 f（x）=a﹣ 
．
（1）證明：f（x）在（﹣∞，+∞）上單調遞增；
（2）若f（x）為奇函數，求：
①a的值；
②f（x）的值域．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】學校藝術節對同一類的
，
，
，
四項參賽作品，只評一項一等獎，在評獎揭曉前，甲、乙、丙、丁四位同學對這四項參賽作品預測如下：
甲說：“是或作品獲得一等獎”；
乙說：“作品獲得一等獎”；
丙說：“，兩項作品未獲得一等獎”；
丁說：“是作品獲得一等獎”.
若這四位同學中只有兩位說的話是對的，則獲得一等獎的作品是__________．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】設函數 
，且其圖象關于直線x=0對稱，則（ ）
A.y=f（x）的最小正周期為π，且在（0， 
）上為增函數
B.y=f（x）的最小正周期為π，且在（0， ）上為減函數
C.y=f（x）的最小正周期為 ，且在 
上為增函數
D.y=f（x）的最小正周期為 ，且在 上為減函數
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
