
【題目】近年空氣質量逐步惡化,霧霾天氣現象出現增多,大氣污染危害加重,大氣污染可引起心悸、呼吸困難等心肺疾病,為了解某市心肺疾病是否與性別有關,在某醫院隨機的對入院50人進行了問卷調查,得到如下的列聯表.
患心肺疾病 | 不患心肺疾病 | 合計 | |
男 | 5 | ||
女 | 10 | ||
合計 | 50 |
已知在全部50人中隨機抽取1人,抽到患心肺疾病的人的概率為 ![]() ,
,
(1)請將上面的列聯表補充完整;
(2)是否有99.5%的把握認為患心肺疾病與性別有關?說明你的理由;
(3)已知在患心肺疾病的10位女性中,有3位又患有胃病,現在從患心肺疾病的10位女性中,選出3名進行其它方面的排查,記選出患胃病的女性人數為ξ,求ξ的分布列、數學期望以及方差.
下面的臨界值表僅供參考:
P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
K | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
【答案】
(1)解:根據在全部50人中隨機抽取1人抽到患心肺疾病生的概率為 ![]() ,可得患心肺疾病的為30人,故可得
,可得患心肺疾病的為30人,故可得
列聯表補充如下
患心肺疾病 | 不患心肺疾病 | 合計 | |
男 | 20 | 5 | 25 |
女 | 10 | 15 | 25 |
合計 | 30 | 20 | 50 |
(2)解:因為 K2= ![]() ,即K2=
,即K2= ![]() =
= ![]() ,
,
所以 K2≈8.333
又 P(k2≥7.879)=0.005=0.5%,
所以,我們有 99.5%的把握認為是否患心肺疾病是與性別有關系的.
(3)解:現在從患心肺疾病的10位女性中,選出3名進行胃病的排查,
記選出患胃病的女性人數為ξ,則ξ=0,1,2,3.
故P(ξ=0)= ![]() =
= ![]() ,P(ξ=1)=
,P(ξ=1)= ![]() =
= ![]() ,P(ξ=2)=
,P(ξ=2)= ![]() =
= ![]() ,P(ξ=3)=
,P(ξ=3)= ![]() ,
,
則ξ的分布列:
ξ | 0 | 1 | 2 | 3 |
P |
|
|
|
|
則Eξ=1× ![]() +2×
+2× ![]() +3×
+3× ![]() =0.9,
=0.9,
Dξ= ![]() ×(0﹣0.9)2+
×(0﹣0.9)2+ ![]() ×(1﹣0.9)2+
×(1﹣0.9)2+ ![]() ×(2﹣0.9)2+
×(2﹣0.9)2+ ![]() ×(3﹣0.9)2=0.49
×(3﹣0.9)2=0.49
【解析】(1)根據在全部50人中隨機抽取1人抽到患心肺疾病的概率為 ![]() ,可得患心肺疾病的人數,即可得到列聯表;(2)利用公式求得K2 , 與臨界值比較,即可得到結論.(3)在患心肺疾病的10位女性中,有3位又患有胃病,記選出患胃病的女性人數為ξ,則ξ服從超幾何分布,即可得到ξ的分布列、數學期望以及方差.
,可得患心肺疾病的人數,即可得到列聯表;(2)利用公式求得K2 , 與臨界值比較,即可得到結論.(3)在患心肺疾病的10位女性中,有3位又患有胃病,記選出患胃病的女性人數為ξ,則ξ服從超幾何分布,即可得到ξ的分布列、數學期望以及方差.


 培優三好生系列答案
培優三好生系列答案 優化作業上海科技文獻出版社系列答案
優化作業上海科技文獻出版社系列答案科目:高中數學 來源: 題型:
【題目】數列![]() 中,已知
中,已知![]() 對任意
對任意![]() 都成立,數列
都成立,數列![]() 的前
的前![]() 項和為
項和為![]() .(這里
.(這里![]() 均為實數)
均為實數)
(1)若![]() 是等差數列,求
是等差數列,求![]() 的值;
的值;
(2)若![]() ,求
,求![]() ;
;
(3)是否存在實數![]() ,使數列
,使數列![]() 是公比不為
是公比不為![]() 的等比數列,且任意相鄰三項
的等比數列,且任意相鄰三項![]() 按某順序排列后成等差數列?若存在,求出所有
按某順序排列后成等差數列?若存在,求出所有![]() 的值;若不存在,請說明理由.
的值;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f (x)=ex-ax-1,其中e為自然對數的底數,a∈R.
(1)若a=e,函數g (x)=(2-e)x.
①求函數h(x)=f (x)-g (x)的單調區間;
②若函數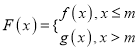 的值域為R,求實數m的取值范圍;
的值域為R,求實數m的取值范圍;
(2)若存在實數x1,x2∈[0,2],使得f(x1)=f(x2),且|x1-x2|≥1,
求證:e-1≤a≤e2-e.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某研究小組到社區了解參加健美操運動人員的情況,用分層抽樣的方法抽取了40人進行調查,按照年齡分成五個小組: ![]() ,并繪制成如圖所示的頻率分布直方圖.
,并繪制成如圖所示的頻率分布直方圖.
(1)求該社區參加健美操運動人員的平均年齡;
(2)如果研究小組從該樣本中年齡在![]() 和
和![]() 的6人中隨機地抽取出2人進行深入采訪,求被采訪的2人,年齡恰好都在
的6人中隨機地抽取出2人進行深入采訪,求被采訪的2人,年齡恰好都在![]() 內的概率.
內的概率.

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】定義在R上的函數f(x)滿足:f(x)+f′(x)>1,f(0)=4,則不等式exf(x)>ex+3(其中e為自然對數的底數)的解集為( )
A.(0,+∞)
B.(﹣∞,0)∪(3,+∞)
C.(﹣∞,0)∪(0,+∞)
D.(3,+∞)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某公司生產一種電子儀器的固定成本為20000元,每生產一臺儀器需增加投入100元,已知總收益函數為R(x)= 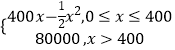 ,其中x是儀器的產量(單位:臺);
,其中x是儀器的產量(單位:臺);
(1)將利潤f(x)表示為產量x的函數(利潤=總收益﹣總成本);
(2)當產量x為多少臺時,公司所獲利潤最大?最大利潤是多少元?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】我國是世界上嚴重缺水的國家,某市政府為了鼓勵居民節約用水,計劃調整居民生活用水收費方案,擬確定一個合理的月用水量標準![]() (噸),一位居民的月用水量不超過
(噸),一位居民的月用水量不超過![]() 的部分按平價收費,超過
的部分按平價收費,超過![]() 的部分按議價收費.為了了解居民用水情況,通過抽樣,獲得了某年100位居民每人的月均用水量(單位:噸),將數據按照
的部分按議價收費.為了了解居民用水情況,通過抽樣,獲得了某年100位居民每人的月均用水量(單位:噸),將數據按照![]() ,
, ![]() ,
, ![]() ,
, ![]() 分成9組,制成了如圖所示的頻率分布直方圖.
分成9組,制成了如圖所示的頻率分布直方圖.
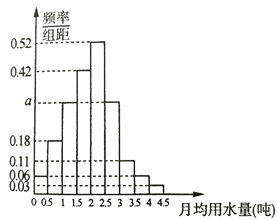
(Ⅰ)求直方圖中![]() 的值;
的值;
(Ⅱ)若將頻率視為概率,從該城市居民中隨機抽取3人,記這3人中月均用水量不低于3噸的人數為![]() ,求
,求![]() 的分布列與數學期望.
的分布列與數學期望.
(Ⅲ)若該市政府希望使85%的居民每月的用水量不超過標準![]() (噸),估計
(噸),估計![]() 的值(精確到0.01),并說明理由.
的值(精確到0.01),并說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com