
【題目】已知拋物線![]() (
(![]() ),焦點
),焦點![]() 到準線的距離為
到準線的距離為![]() ,過點
,過點![]()
![]() 作直線
作直線![]() 交拋物線
交拋物線![]() 于點
于點![]() (點
(點![]() 在第一象限).
在第一象限).
(Ⅰ)若點![]() 焦點
焦點![]() 重合,且弦長
重合,且弦長![]() ,求直線
,求直線![]() 的方程;
的方程;
(Ⅱ)若點![]() 關于
關于![]() 軸的對稱點為
軸的對稱點為![]() ,直線
,直線![]() 交x軸于點
交x軸于點![]() ,且
,且![]() ,求證:點B的坐標是
,求證:點B的坐標是![]() ,并求點
,并求點![]() 到直線
到直線![]() 的距離
的距離![]() 的取值范圍.
的取值范圍.
【答案】(Ⅰ) ![]() 或
或![]() .(Ⅱ)
.(Ⅱ) 
【解析】
試題分析:(Ⅰ)確定拋物線的方程,設出直線方程與拋物線方程聯立,利用弦長|PQ|=2,即可求直線l的方程;(Ⅱ)設出直線方程與拋物線方程聯立,利用韋達定理,結合向量知識,證明B(-![]() ,0),確定出
,0),確定出![]() ,或m的范圍,表示出點B到直線l的距離d,即可求得取值范圍
,或m的范圍,表示出點B到直線l的距離d,即可求得取值范圍
試題解析:(Ⅰ)解:由題意可知,![]() ,故拋物線方程為
,故拋物線方程為![]() ,焦點
,焦點![]() .
.
設直線l的方程為![]() ,
,![]()
![]() ,
,![]() .
.
由 消去x,得
消去x,得![]() .所以△=n2+1>0,
.所以△=n2+1>0,![]() .
.
因為![]() ,點A與焦點F重合,
,點A與焦點F重合,
所以![]() .
.
所以n2=1,即n=±1.所以直線l的方程為![]() 或
或![]() ,
,
即![]() 或
或![]() .
.
(Ⅱ)證明:設直線l的方程為![]() (m≠0),
(m≠0),![]() ,
,![]() 則
則![]()
由 消去x,得
消去x,得![]() ,
,
因為![]() ,所以△=m2+4x0>0,y1+y2=m,y1y2=-x0.
,所以△=m2+4x0>0,y1+y2=m,y1y2=-x0.
設B(xB,0),則![]() .
.
由題意知,![]() ,所以
,所以![]() ,
,
即![]() .
.
顯然![]() ,所以
,所以![]() ,即證B(-x0,0).
,即證B(-x0,0).
由題意知,△MBQ為等腰直角三角形,所以![]() ,即
,即![]() ,也即
,也即![]() ,
,
所以![]() ,所以
,所以![]() ,
,
即![]() ,所以
,所以![]() >0,即
>0,即![]()
又因為![]() ,所以
,所以![]() .
. ,
,
所以d的取值范圍是 .
.


 期末好成績系列答案
期末好成績系列答案 99加1領先期末特訓卷系列答案
99加1領先期末特訓卷系列答案 百強名校期末沖刺100分系列答案
百強名校期末沖刺100分系列答案 好成績1加1期末沖刺100分系列答案
好成績1加1期末沖刺100分系列答案 金狀元績優好卷系列答案
金狀元績優好卷系列答案科目:高中數學 來源: 題型:
【題目】(本小題滿分14分)體育測試成績分為四個等級:優、良、中、不及格.某班50名學生參加測試的結果如下:
等級 | 優 | 良 | 中 | 不及格 |
人數 | 5 | 19 | 23 | 3 |
(1)從該班任意抽取1名學生,求這名學生的測試成績為“良”或“中”的概率;
(2)測試成績為“優”的3名男生記為![]() ,
,![]() ,
,![]() ,2名女生記為
,2名女生記為![]() ,
,![]() .現從這5人中任選2人參加學校的某項體育比賽.
.現從這5人中任選2人參加學校的某項體育比賽.
① 寫出所有等可能的基本事件;
② 求參賽學生中恰有1名女生的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為了普及法律知識,達到“法在心中”的目的,某市法制辦組織了普法知識競賽.統計局調查隊隨機抽取了甲、乙兩單位中各5名職工的成績,成績如下表:
甲單位 | 87 | 88 | 91 | 91 | 93 |
乙單位 | 85 | 89 | 91 | 92 | 93 |
(1)根據表中的數據,分別求出甲、乙兩單位職工成績的平均數和方差,并判斷哪個單位對法律知識的掌握更穩定;
(2)用簡單隨機抽樣法從乙單位5名職工中抽取2名,他們的成績組成一個樣本,求抽取的2名職工的分數差至少是4的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】心理學家發現,學生的接受能力依賴于老師引入概念和描述問題所用的時間,上課開始時,學生的興趣激增,中間有一段不太長的時間,學生的興趣保持較理想的狀態,隨后學生的注意力開始分散,并趨于穩定.分析結果和實驗表明,設提出和講述概念的時間為![]() (單位:分),學生的接受能力為
(單位:分),學生的接受能力為![]() (
(![]() 值越大,表示接受能力越強),
值越大,表示接受能力越強),
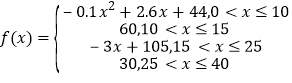
(1)開講后多少分鐘,學生的接受能力最強?能維持多少時間?
(2)試比較開講后5分鐘、20分鐘、35分鐘,學生的接受能力的大小;(3)若一個數學難題,需要56的接受能力以及12分鐘時間,老師能否及時在學生一直達到所需接受能力的狀態下講述完這個難題?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知直線![]() (
(![]() ).
).
(1)證明:直線![]() 過定點;
過定點;
(2)若直線不經過第四象限,求![]() 的取值范圍;
的取值范圍;
(3)若直線![]() 軸負半軸于
軸負半軸于![]() ,交
,交![]() 軸正半軸于
軸正半軸于![]() ,△
,△![]() 的面積為
的面積為![]() (
(![]() 為坐標原點),求
為坐標原點),求![]() 的最小值,并求此時直線
的最小值,并求此時直線![]() 的方程.
的方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為了對某課題進行研究,用分層抽樣方法從三所高校![]() 的相關人員中,抽取若干人組成研究小組,有關數據見下表(單位:人)
的相關人員中,抽取若干人組成研究小組,有關數據見下表(單位:人)
高校 | 相關人數 | 抽取人數 |
A | 18 |
|
B | 36 | 2 |
C | 54 |
|
(Ⅰ)求![]() ,
,![]() ;
;
(Ⅱ)若從高校![]() 抽取的人中選2人作專題發言,求這二人都來自高校
抽取的人中選2人作專題發言,求這二人都來自高校![]() 的概率.
的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在三棱柱ABCA1B1C1中, CC1⊥平面ABC, AC⊥BC, AB1的中點為D,B1C∩BC1=E. 求證:
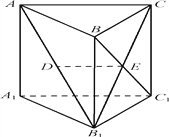
(1)DE∥平面AA1C1C;
(2)AC⊥平面BCC1B1.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】(本小題滿分14分)
在四棱錐P-ABCD中,BC∥AD,PA⊥PD,AD=2BC,AB=PB, E為PA的中點.
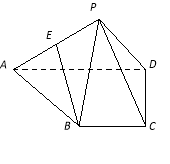
(1)求證:BE∥平面PCD;
(2)求證:平面PAB⊥平面PCD.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知點![]() ,點
,點![]() 是圓
是圓![]()
![]() 上的任意一點,線段
上的任意一點,線段![]() 的垂直平分線與直線
的垂直平分線與直線![]() 交于點
交于點![]() .
.
(Ⅰ)求點![]() 的軌跡方程;
的軌跡方程;
(Ⅱ)若直線![]() 與點
與點![]() 的軌跡有兩個不同的交點
的軌跡有兩個不同的交點![]() 和
和![]() ,且原點
,且原點![]() 總在以
總在以![]() 為直徑的圓的內部,求實數
為直徑的圓的內部,求實數![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com