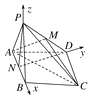
【題目】如圖，已知四棱錐P－ABCD，底面ABCD為菱形，且∠DAB＝60°，△PAB是邊長為a的正三角形，且平面PAB⊥平面ABCD，已知點(diǎn)M是PD的中點(diǎn)．
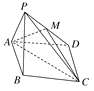
(1)證明：PB∥平面AMC；
(2)求直線BD與平面AMC所成角的正弦值．
【答案】（1）見解析；（2）
【解析】試題分析：（1）連接BD交AC于點(diǎn)O，由三角形中位線可得OM∥PB. 再根據(jù)線面平行判定定理得結(jié)論（2）先根據(jù)空間直角坐標(biāo)系，再設(shè)立各點(diǎn)坐標(biāo)，根據(jù)方程組解得平面法向量，根據(jù)向量數(shù)量積求向量夾角，最后根據(jù)線面角與向量夾角互余關(guān)系得結(jié)果．
試題解析：(1)證明：連接BD交AC于點(diǎn)O，連接OM，因?yàn)樗倪呅?/span>ABCD為菱形，OB＝OD，又M為PD的中點(diǎn)，所以OM∥PB.
由PB平面AMC，OM平面AMC，所以PB∥平面ACM.
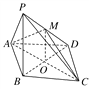
(2)取AB的中點(diǎn)N，連接PN，ND，則∠AND＝90°，
分別以NB，ND，NP為x軸、y軸、z軸建立空間直角坐標(biāo)系N－xyz，
則B
，C
，
A
，D
，P
，M
，
則
＝
，
＝
.
設(shè)平面AMC的法向量為n＝(x，y，z)，
則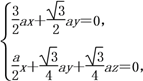
令y＝
，則x＝－1，
z＝－
，即n＝
.又
＝
，設(shè)直線BD與n所成的角為θ，則cosθ＝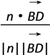
＝
，故直線BD與平面AMC所成角的正弦值為.
閱讀快車系列答案
| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦！ | 初一 | 初一免費(fèi)課程推薦！ |
| 高二 | 高二免費(fèi)課程推薦！ | 初二 | 初二免費(fèi)課程推薦！ |
| 高三 | 高三免費(fèi)課程推薦！ | 初三 | 初三免費(fèi)課程推薦！ |
科目：高中數(shù)學(xué) 來源： 題型：
【題目】已知數(shù)集
（
，
）具有性質(zhì)
：對任意
、
（
），
與
兩數(shù)中至少有一個屬于集合
，現(xiàn)給出以下四個命題：①數(shù)集
具有性質(zhì)；②數(shù)集
具有性質(zhì)；③若數(shù)集具有性質(zhì)，則
；④若數(shù)集
（
）具有性質(zhì)，則
；其中真命題有________（填寫序號）
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】某零售公司從1月至6月的銷售量與利潤的統(tǒng)計數(shù)據(jù)如下：
月份 | 1 | 2 | 3 | 4 | 5 | 6 |
銷售量 | 6 | 8 | 12 | 13 | 11 | 10 |
利潤 | 12 | 16 | 26 | 29 | 25 | 22 |
（1）根據(jù)2月至5月4個月的統(tǒng)計數(shù)據(jù)，求出
關(guān)于
的回歸直線方程
.（
的結(jié)果用分?jǐn)?shù)表示）；
（2）若由回歸直線方程得到的估計數(shù)據(jù)與實(shí)際數(shù)據(jù)的誤差均不超過1萬元，則認(rèn)為得到的回歸直線方程是有效的.試用1月和6月的數(shù)據(jù)估計所得的回歸直線方程是否有效？
參考公式：
，
.
參考數(shù)據(jù)：
，
.
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】某漁業(yè)公司今年初用98萬元購進(jìn)一艘漁船進(jìn)行捕撈，第一年需要各種費(fèi)用12萬元，從第二年開始包括維修費(fèi)在內(nèi)，每年所需費(fèi)用均比上一年增加4萬元，該船每年捕撈的總收入為50萬元.
（1）該船捕撈第幾年開始盈利？
（2）若該船捕撈
年后，年平均盈利達(dá)到最大值，該漁業(yè)公司以24萬元的價格將捕撈船賣出；求并求總的盈利值.
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】太極圖是由黑白兩個魚形紋組成的圖案，太極圖展現(xiàn)了一種相互轉(zhuǎn)化，相互統(tǒng)一的和諧美.定義：能夠?qū)A
的周長和面積同時等分成兩部分的函數(shù)稱為圓的一個“太極函數(shù)”.下列有關(guān)說法中正確的個數(shù)是（ ）個
①對圓
的所有非常數(shù)函數(shù)的太極函數(shù)中，一定不能為偶函數(shù)；
②函數(shù)
是圓
的一個太極函數(shù)；
③存在圓，使得
是圓的太極函數(shù)；
④直線
所對應(yīng)的函數(shù)一定是圓
的太極函數(shù).
A.
B.
C.
D.
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】如圖，在三棱錐PABC中，PA⊥底面ABC，∠BAC＝90°.點(diǎn)D，E，N分別為棱PA，PC，BC的中點(diǎn)，M是線段AD的中點(diǎn)，PA＝AC＝4，AB＝2.
(1)求證：MN∥平面BDE；
(2)求二面角CEMN的正弦值；
(3)已知點(diǎn)H在棱PA上，且直線NH與直線BE所成角的余弦值為
，求線段AH的長．
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】已知
是定義在
上的奇函數(shù).
（1）當(dāng)
時， 
，若當(dāng)
時， 
恒成立，求
的最小值；
（2）若
的圖像關(guān)于
對稱，且
時， 
，求當(dāng)
時， 的解析式；
（3）當(dāng)
時， 
.若對任意的
，不等式
恒成立，求實(shí)數(shù)
的取值范圍.
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】下列幾個命題：①若方程
的兩個根異號，則實(shí)數(shù)
；②函數(shù)
是偶函數(shù)，但不是奇函數(shù)；③函數(shù) 
在
上是減函數(shù)，則實(shí)數(shù)a的取值范圍是
；④ 方程 
的根
滿足
，則m滿足的范圍
，其中不正確的是（ ）
A.①B.②C.③D.④
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】設(shè)二次函數(shù)
滿足下列條件：當(dāng)
時，
的最小值為0，且
成立；當(dāng)
時，
恒成立.
（1）求的解析式；
（2）若對
，不等式
恒成立、求實(shí)數(shù)
的取值范圍；
（3）求最大的實(shí)數(shù)
，使得存在實(shí)數(shù)
，只要當(dāng)
時，就有
成立.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com