
【題目】已知函數(shù)![]() .
.
(1)求曲線![]() 在點
在點![]() 處的切線方程;
處的切線方程;
(2)求![]() 的單調(diào)區(qū)間;
的單調(diào)區(qū)間;
(3)若對于任意![]() ,都有
,都有![]() ,求實數(shù)
,求實數(shù)![]() 的取值范圍.
的取值范圍.
【答案】(1)![]() ;(2)
;(2)![]() 的增區(qū)間是
的增區(qū)間是![]() ;
;
遞減區(qū)間是![]() ;(3)
;(3)![]() .
.
【解析】試題分析:(1)求出![]() 的值可得切點坐標,再求出
的值可得切點坐標,再求出![]() ,可得
,可得![]() 的值,即得切線斜率,利用點斜式可得曲線
的值,即得切線斜率,利用點斜式可得曲線![]() 在點
在點![]() 處的切線方程;(2)令
處的切線方程;(2)令![]() 求得
求得![]() 的范圍,可得函數(shù)
的范圍,可得函數(shù)![]() 增區(qū)間,
增區(qū)間, ![]() 求得
求得![]() 的范圍,可得函數(shù)
的范圍,可得函數(shù)![]() 的減區(qū)間;(3)對于任意
的減區(qū)間;(3)對于任意![]() ,都有
,都有![]() 等價于
等價于![]() ,令
,令![]() ,
, ![]() ,利用導數(shù)研究函數(shù)
,利用導數(shù)研究函數(shù)![]() 的單調(diào)性,求出函數(shù)
的單調(diào)性,求出函數(shù)![]() 的最大值,從而可得結(jié)果.
的最大值,從而可得結(jié)果.
試題解析:(1)因為函數(shù)![]() ,所以
,所以![]() ,
,
![]() .又因為
.又因為![]() ,
,
所以曲線![]() 在點
在點![]() 處的切線方程為
處的切線方程為![]() .
.
(2)函數(shù)![]() 定義域為
定義域為![]() , 由(1)可知,
, 由(1)可知, ![]() .
.
令![]() 解得
解得![]() .
.
![]() 與
與![]() 在區(qū)間
在區(qū)間![]() 上的情況如下:
上的情況如下:
|
|
|
|
|
|
|
|
| 減 | 極小值 | 增 |
所以, ![]() 的單調(diào)遞增區(qū)間是
的單調(diào)遞增區(qū)間是![]() ;
;
![]() 的單調(diào)遞減區(qū)間是
的單調(diào)遞減區(qū)間是![]() .
.
(3)當![]() 時,“
時,“![]() ”等價于“
”等價于“![]() ”.
”.
令![]() ,
, ![]() ,
,
![]() ,
, ![]() .
.
當![]() 時,
時, ![]() ,所以
,所以![]() 在區(qū)間
在區(qū)間![]() 單調(diào)遞減.
單調(diào)遞減.
當![]() 時,
時, ![]() ,所以
,所以![]() 在區(qū)間
在區(qū)間![]() 單調(diào)遞增.
單調(diào)遞增.
而![]() ,
,
![]() .
.
所以![]() 在區(qū)間
在區(qū)間![]() 上的最大值為
上的最大值為![]() .
.
所以當![]() 時,對于任意
時,對于任意![]() ,都有
,都有![]() .
.
【方法點晴】本題主要考查利用導數(shù)求曲線切線方程以及利用導數(shù)研究函數(shù)的單調(diào)性與不等式恒成立問題,屬于難題.不等式恒成立問題常見方法:① 分離參數(shù)![]() 恒成立(
恒成立(![]() 可)或
可)或![]() 恒成立(
恒成立(![]() 即可);② 數(shù)形結(jié)合(
即可);② 數(shù)形結(jié)合(![]() 圖象在
圖象在![]() 上方即可);③ 討論最值
上方即可);③ 討論最值![]() 或
或![]() 恒成立;④ 討論參數(shù).本題(3)是利用方法 ① 求得實數(shù)
恒成立;④ 討論參數(shù).本題(3)是利用方法 ① 求得實數(shù)![]() 的取值范圍.
的取值范圍.


科目:高中數(shù)學 來源: 題型:
【題目】某次有600人參加的數(shù)學測試,其成績的頻數(shù)分布表如圖所示,規(guī)定85分及其以上為優(yōu)秀.
區(qū)間 | [75,80) | [80,85) | [85,90) | [90,95) | [95,100] |
人數(shù) | 36 | 114 | 244 | 156 | 50 |
(Ⅰ)現(xiàn)用分層抽樣的方法從這600人中抽取20人進行成績分析,求其中成績?yōu)閮?yōu)秀的學生人數(shù);
(Ⅱ)在(Ⅰ)中抽取的20名學生中,要隨機選取2名學生參加活動,記“其中成績?yōu)閮?yōu)秀的人數(shù)”為![]() ,求
,求![]() 的分布列與數(shù)學期望.
的分布列與數(shù)學期望.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
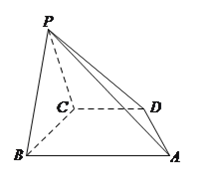
【題目】在四棱錐![]() 中,底面
中,底面![]() 是直角梯形,
是直角梯形, ![]() ,
, ![]() ,
, ![]() ,平面
,平面![]() 平面
平面![]() .
.
(Ⅰ)求證: ![]() 平面
平面![]() .
.
(Ⅱ)求平面![]() 和平面
和平面![]() 所成二面角(小于
所成二面角(小于![]() )的大小.
)的大小.
(Ⅲ)在棱![]() 上是否存在點
上是否存在點![]() 使得
使得![]() 平面
平面![]() ?若存在,求
?若存在,求![]() 的值;若不存在,請說明理由.
的值;若不存在,請說明理由.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】如圖,在四棱錐PABCD中,AB∥CD ,且∠BAP=∠CDP =90°.
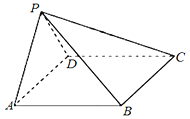
(1).證明:平面PAB⊥平面PAD;
(2).若PA=PD=AB=DC, ∠APD =90°,且四棱錐PABCD的體積為![]() ,求該四棱錐的側(cè)面積.
,求該四棱錐的側(cè)面積.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】選修4-4:坐標系與參數(shù)方程
已知曲線![]() 的參數(shù)方程為
的參數(shù)方程為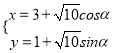 (
(![]() 為參數(shù)),以直角坐標系原點
為參數(shù)),以直角坐標系原點![]() 為極點,以
為極點,以![]() 軸正半軸為極軸,建立極坐標系.
軸正半軸為極軸,建立極坐標系.
(1)求曲線![]() 的極坐標方程,并說明其表示什么軌跡;
的極坐標方程,并說明其表示什么軌跡;
(2)若直線的極坐標方程為![]() ,求直線被曲線
,求直線被曲線![]() 截得的弦長.
截得的弦長.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】選修4-4:坐標系與參數(shù)方程
已知直線![]() 的極坐標方程是
的極坐標方程是![]() ,以極點為原點,極軸為
,以極點為原點,極軸為![]() 軸的正半軸建立極坐標系,曲線
軸的正半軸建立極坐標系,曲線![]() 的參數(shù)方程為
的參數(shù)方程為![]() (
(![]() 為參數(shù)).
為參數(shù)).
(1)寫出直線![]() 的普通方程與曲線
的普通方程與曲線![]() 的直角坐標方程;
的直角坐標方程;
(2)設(shè)![]() 為曲線
為曲線![]() 上任意一點,求
上任意一點,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知函數(shù)![]() ,
, ![]()
![]() .
.
(I)當a=2時,求曲線y = ![]() 在點(0,f(0))處的切線方程;
在點(0,f(0))處的切線方程;
(II)求函數(shù)![]() 在區(qū)間[0 , e -1]上的最小值.
在區(qū)間[0 , e -1]上的最小值.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知點![]() 在橢圓
在橢圓![]() 上,且橢圓的離心率為
上,且橢圓的離心率為![]() .
.
(1)求橢圓![]() 的方程;
的方程;
(2)若![]() 為橢圓
為橢圓![]() 的右頂點,點
的右頂點,點![]() 是橢圓
是橢圓![]() 上不同的兩點(均異于
上不同的兩點(均異于![]() )且滿足直線
)且滿足直線![]() 與
與![]() 斜率之積為
斜率之積為![]() .試判斷直線
.試判斷直線![]() 是否過定點,若是,求出定點坐標,若不是,說明理由.
是否過定點,若是,求出定點坐標,若不是,說明理由.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知拋物線![]() 的準線與
的準線與![]() 軸交于點
軸交于點![]() ,過點
,過點![]() 做圓
做圓![]() 的兩條切線,切點為
的兩條切線,切點為![]() .
.
(1)求拋物線![]() 的方程;
的方程;
(2)若直線![]() 是講過定點
是講過定點![]() 的一條直線,且與拋物線
的一條直線,且與拋物線![]() 交于
交于![]() 兩點,過定點
兩點,過定點![]() 作
作![]() 的垂線與拋物線交于
的垂線與拋物線交于![]() 兩點,求四邊形
兩點,求四邊形![]() 面積的最小值.
面積的最小值.
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com