【題目】某闖關游戲規劃是:先后擲兩枚骰子，將此試驗重復
輪，第輪的點數分別記為
，如果點數滿足
，則認為第輪闖關成功，否則進行下一輪投擲，直到闖關成功，游戲結束.
(1)求第1輪闖關成功的概率；
(2)如果第
輪闖關成功所獲的獎金(單位:元) 
，求某人闖關獲得獎金不超過2500元的概率；
(3)如果游戲只進行到第4輪，第4輪后無論游戲成功與否，都終止游戲，記進行的輪數為隨機變量
，求的分布列和數學期望.
【答案】（1）
（2）見解析(3)見解析
【解析】
（1）枚舉法列出所有滿足條件的數對
即可；
（2）由
，得
，由（1）每輪過關的概率為，某人闖關獲得獎金不超過2500元的概率：
；
（3）設游戲第
輪后終止的概率為
，分別求出相應的概率，由此能求出X的分布列和數學期望.
解:(1)若第1輪闖關成功，
當
時， 
，因此
；
當
時， 
，因此；
當
時，
，因此；
當
時，
，因此
；
當
時， 
，因此；
當
時， 
，因此
無值.
記“第1輪闖關成功”為事件
，
則第1輪闖關成功的概率
.
(2)由，得，
由(1)知每輪闖關成功的概率為.
某人闖關獲得獎金不超過2500元的概率
.
(3)依題意
的所有可能取值為1，2，3，4，
設游戲第輪后終止的概率為，
則
，
，
，
.
故的分布列為
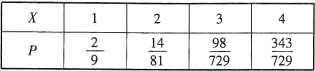
因此數學期望
.
科目：高中數學 來源： 題型：
【題目】選修4-4：坐標系與參數方程
在直角坐標系
中，曲線
的參數方程為
（
為參數），在以坐標原點為極點，
軸正半軸為極軸的極坐標系中，直線
的極坐標方程為
.
（1）求曲線和直線在該直角坐標系下的普通方程；
（2）動點
在曲線上，動點
在直線上，定點
的坐標為
，求
的最小值.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知拋物線
（
）與雙曲線
（
，
）有相同的焦點
，點
是兩條曲線的一個交點，且
軸，則該雙曲線經過一、三象限的漸近線的傾斜角所在的區間是（ ）
A. 
B. 
C. 
D. 
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某兒童樂園在“六一”兒童節推出了一項趣味活動.參加活動的兒童需轉動如圖所示的轉盤兩次，每次轉動后，待轉盤停止轉動時，記錄指針所指區域中的數.設兩次記錄的數分別為x，y.獎勵規則如下：
①若
，則獎勵玩具一個；
②若
，則獎勵水杯一個；
③其余情況獎勵飲料一瓶.
假設轉盤質地均勻，四個區域劃分均勻.小亮準備參加此項活動.
（Ⅰ）求小亮獲得玩具的概率；
（Ⅱ）請比較小亮獲得水杯與獲得飲料的概率的大小，并說明理由.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】設函數f（x）＝2ax2+2bx，若存在實數x0∈（0，t），使得對任意不為零的實數a，b均有f（x0）＝a+b成立，則t的取值范圍是_____．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某市2016年6月30天的空氣質量指數如下：
35 | 54 | 80 | 86 | 72 | 85 | 58 | 125 | 111 | 53 |
10 | 66 | 46 | 36 | 18 | 25 | 23 | 40 | 60 | 89 |
88 | 54 | 79 | 14 | 16 | 40 | 59 | 67 | 111 | 62 |
你覺得這個月的空氣質量如何？請設計適當的頻率分布直方圖展示這組數據，并結合空氣質量分級標準分析數據.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知直線
的參數方程為
（
為參數），曲線
的參數方程為
（為參數），以坐標原點為極點，
軸的正半軸為極軸建立極坐標系，且曲線
的極坐標方程為
.
（1）若直線的斜率為
，判斷直線與曲線的位置關系；
（2）求與交點的極坐標（
，
）.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
