
在直角梯形ABCD中,AD//BC,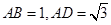 ,
,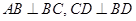 ,如圖(1).把
,如圖(1).把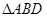 沿
沿 翻折,使得平面
翻折,使得平面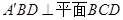 ,如圖(2).
,如圖(2).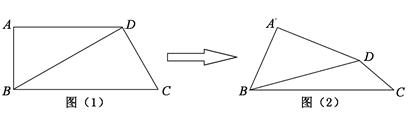
(Ⅰ)求證: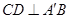 ;
;
(Ⅱ)求三棱錐 的體積;
的體積;
(Ⅲ)在線段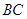 上是否存在點N,使得
上是否存在點N,使得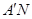
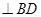 ?若存在,請求出
?若存在,請求出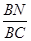 的值;若不存在,請說明理由.
的值;若不存在,請說明理由.
(1)根據題意中的平面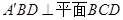 ,可知得到
,可知得到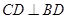 ,進而得到
,進而得到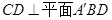 ,根據線面垂直的性質定理得到結論。
,根據線面垂直的性質定理得到結論。
(2)
(3)在線段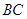 上存在點N,使得
上存在點N,使得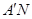
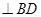 ,此時
,此時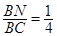
解析試題分析:解:(Ⅰ)∵平面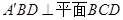 ,
,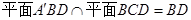 ,
,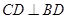
∴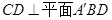 , 2分
, 2分
又∵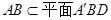 ,∴
,∴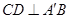 . 4分
. 4分
(Ⅱ)如圖(1)在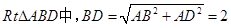 .
.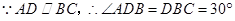 .
.
在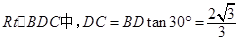 .
.
∴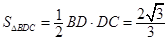 . 6分
. 6分
如圖(2),在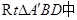 ,過點
,過點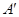 做
做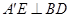 于
于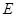 ,∴
,∴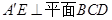 .
.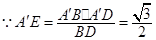 , 7分
, 7分
∴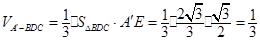 . 8分
. 8分
(Ⅲ)在線段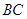 上存在點N,使得
上存在點N,使得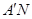
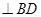 ,理由如下:
,理由如下:
如圖(2)在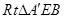 中,
中,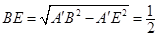 ,
,
∴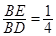 , 9分
, 9分
過點E做 交
交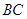 于點N,則
于點N,則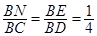 ,
,
∵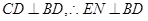 , 10分
, 10分
又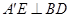 ,
,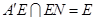 ,
,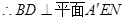 ,
,
又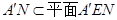 ,∴
,∴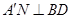 .
.
∴在線段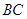 上存在點N,使得
上存在點N,使得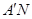
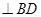 ,此時
,此時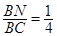 . 12分
. 12分
考點:直線與直線、直線與平面的位置關系
點評:本小題主要考查直線與直線、直線與平面的位置關系、棱錐體積公式等基礎知識,考查空間想象能力、推理論證能力及運算求解能力,考查化歸與轉化思想、數形結合思想


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:高中數學 來源: 題型:解答題
如圖,平面四邊形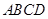 的4個頂點都在球
的4個頂點都在球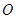 的表面上,
的表面上,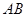 為球
為球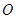 的直徑,
的直徑, 為球面上一點,且
為球面上一點,且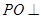 平面
平面 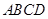 ,
,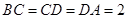 ,點
,點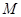 為
為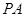 的中點.
的中點.
(1) 證明:平面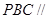 平面
平面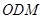 ;
;
(2) 求平面 與平面
與平面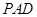 所成銳二面角的余弦值.
所成銳二面角的余弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
如圖一,△ABC是正三角形,△ABD是等腰直角三角形,AB=BD=2。將△ABD沿邊AB折起, 使得△ABD與△ABC成30o的二面角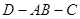 ,如圖二,在二面角
,如圖二,在二面角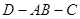 中.
中.
(1) 求CD與面ABC所成的角正弦值的大小;
(2) 對于AD上任意點H,CH是否與面ABD垂直。
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
如圖,在四棱柱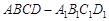 中,側棱
中,側棱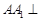 底面
底面 ,
,
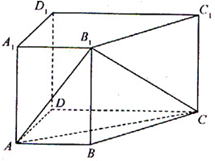
(Ⅰ)求證: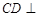 平面
平面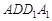
(Ⅱ)若直線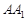 與平面
與平面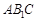 所成角的正弦值為
所成角的正弦值為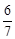 ,求
,求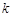 的值
的值
(Ⅲ)現將與四棱柱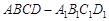 形狀和大小完全相同的兩個四棱柱拼成一個新的四棱柱,規定:若拼成的新四棱柱形狀和大小完全相同,則視為同一種拼接方案,問共有幾種不同的拼接方案?在這些拼接成的新四棱柱中,記其中最小的表面積為
形狀和大小完全相同的兩個四棱柱拼成一個新的四棱柱,規定:若拼成的新四棱柱形狀和大小完全相同,則視為同一種拼接方案,問共有幾種不同的拼接方案?在這些拼接成的新四棱柱中,記其中最小的表面積為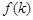 ,寫出
,寫出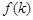 的解析式。(直接寫出答案,不必說明理由)
的解析式。(直接寫出答案,不必說明理由)
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
正四棱錐 中,
中,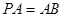 ,點M,N分別在PA,BD上,且
,點M,N分別在PA,BD上,且 .
.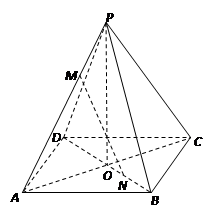
(Ⅰ)求異面直線MN與AD所成角;
(Ⅱ)求證: ∥平面PBC;
∥平面PBC;
(Ⅲ)求MN與平面PAB所成角的正弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
如圖,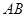 是半圓
是半圓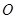 的直徑,
的直徑, 是半圓
是半圓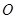 上除
上除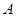 、
、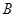 外的一個動點,
外的一個動點,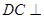 平面
平面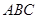 ,
,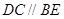 ,
,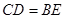 ,
,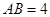 ,
,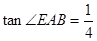 .
.
⑴證明:平面 平面
平面 ;
;
⑵試探究當 在什么位置時三棱錐
在什么位置時三棱錐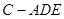 的體積取得最大值,請說明理由并求出這個最大值.
的體積取得最大值,請說明理由并求出這個最大值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com