Question

【題目】如圖所示，在四棱錐中， ， 都是等邊三角形，平面平面，且， .

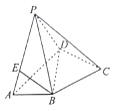
（Ⅰ）求證：平面平面；

（Ⅱ）是上一點，當平面時，三棱錐的體積.

Answer 1

【答案】(Ⅰ)證明見解析；(Ⅱ)6.

【解析】試題分析：

（Ⅰ）要證面面垂直，一般先證線面垂直，也就要證線線垂直，經過計算，得出，從而有，即，于是有面面垂直的性質知，從而得證面面垂直；

（Ⅱ）要求三棱錐的體積，關鍵是找出E點的位置，由于平面，可以過BE作與平面PCD平行的平面，交AD于G，則BG//CD，EG//PD，由已知可知，　確定了G點，就可確定E點位置，從而求出E到平面PCD的距離，再求得面積，就有，從而得所求體積．

試題解析：

（Ⅰ）因為， ， ，

所以，所以， ，

又因為是等邊三角形，所以，所以，

因為平面平面，平面平面，

所以平面，

因為平面，所以平面.

（Ⅱ）過點作交于，過點作交于，

因為， 平面， 平面，所以平面，

同理可得平面，所以平面平面，

因為平面，所以平面.

因為，所以，在直角三角形中， ， ，

所以，所以，

在平面內過作于，

因為平面， 平面，所以，

因為，所以平面，所以是點到平面的距離，

過點作于，則，

由，得，所以，

因為，所以.