
下表給出一個(gè)“三角形數(shù)陣”.已知每一列數(shù)成等差數(shù)列,從第三行起,每一行數(shù)成等比數(shù)列,而且每一行的公比都相等,記第i行第j列的數(shù)為aij(i≥j,i,j∈N*),則a53等于 ,amn= (m≥3).
 ,
,
 ,
,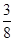 ,
,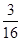
…
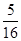
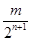
解析



| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來(lái)源: 題型:填空題
數(shù)列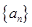 的前
的前 項(xiàng)和為
項(xiàng)和為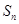 .若數(shù)列
.若數(shù)列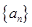 的各項(xiàng)按如下規(guī)則排列:
的各項(xiàng)按如下規(guī)則排列: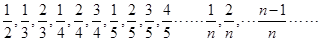 則
則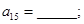 若存在正整數(shù)
若存在正整數(shù)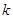 ,使
,使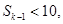
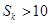 ,則
,則
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:填空題
用數(shù)學(xué)歸納法證明“當(dāng)n為正奇數(shù)時(shí),xn+yn能被x+y整除”的第二步是____.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:填空題
用數(shù)學(xué)歸納法證明 ≥
≥ n(a,b是非負(fù)實(shí)數(shù),n∈N+)時(shí),假設(shè)n
n(a,b是非負(fù)實(shí)數(shù),n∈N+)時(shí),假設(shè)n
=k命題成立之后,證明n=k+1命題也成立的關(guān)鍵是________________.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:填空題
對(duì)于大于1的自然數(shù)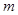 的三次冪可用奇數(shù)進(jìn)行以下方式的“分裂”:
的三次冪可用奇數(shù)進(jìn)行以下方式的“分裂”: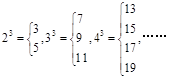 .仿此,若
.仿此,若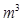 的“分裂數(shù)”中有一個(gè)是2015,則
的“分裂數(shù)”中有一個(gè)是2015,則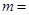 .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:填空題
)在計(jì)算“1×2+2×3+…+n(n+1)”時(shí),某同學(xué)學(xué)到了如下一種方法:先改寫(xiě)第k項(xiàng):
k(k+1)=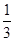 [k(k+1)(k+2)-(k-1)k(k+1)],
[k(k+1)(k+2)-(k-1)k(k+1)],
由此得1×2=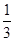 (1×2×3-0×1×2),
(1×2×3-0×1×2),
2×3=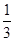 (2×3×4-1×2×3),…,
(2×3×4-1×2×3),…,
n(n+1)=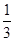 [n(n+1)(n+2)-(n-1)n(n+1)].
[n(n+1)(n+2)-(n-1)n(n+1)].
相加,得1×2+2×3+…+n(n+1)=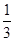 n(n+1)(n+2).
n(n+1)(n+2).
類(lèi)比上述方法,請(qǐng)你計(jì)算“1×2×3+2×3×4+…+n(n+1)(n+2)”,其結(jié)果為 .
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:填空題
對(duì)于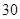 個(gè)互異的實(shí)數(shù),可以排成
個(gè)互異的實(shí)數(shù),可以排成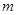 行
行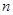 列的矩形數(shù)陣,右圖所示的
列的矩形數(shù)陣,右圖所示的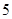 行
行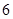 列的矩形數(shù)陣就是其中之一.將
列的矩形數(shù)陣就是其中之一.將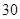 個(gè)互異的實(shí)數(shù)排成
個(gè)互異的實(shí)數(shù)排成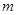 行
行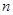 列的矩形數(shù)陣后,把每行中最大的數(shù)選出,記為
列的矩形數(shù)陣后,把每行中最大的數(shù)選出,記為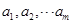 ,并設(shè)其中最小的數(shù)為
,并設(shè)其中最小的數(shù)為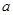 ;把每列中最小的數(shù)選出,記為
;把每列中最小的數(shù)選出,記為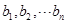 ,并設(shè)其中最大的數(shù)為
,并設(shè)其中最大的數(shù)為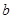 .
.
兩位同學(xué)通過(guò)各自的探究,分別得出兩個(gè)結(jié)論如下:
①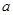 和
和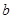 必相等; ②
必相等; ②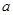 和
和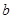 可能相等;
可能相等;
③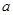 可能大于
可能大于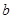 ; ④
; ④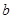 可能大于
可能大于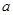 .
.
以上四個(gè)結(jié)論中,正確結(jié)論的序號(hào)是__________________(請(qǐng)寫(xiě)出所有正確結(jié)論的序號(hào)).
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:填空題
觀(guān)察下列等式: +
+ =1;
=1;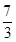 +
+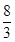 +
+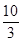 +
+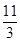 =12;
=12; +
+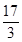 +
+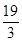 +
+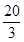 +
+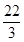 +
+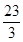 =39;
=39;
……
則當(dāng)m<n且m,n∈N時(shí),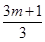 +
+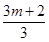 +
+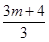 +
+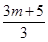 +…+
+…+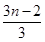 +
+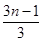 =________(最后結(jié)果用m,n表示).
=________(最后結(jié)果用m,n表示).
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專(zhuān)區(qū) | 電信詐騙舉報(bào)專(zhuān)區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專(zhuān)區(qū) | 涉企侵權(quán)舉報(bào)專(zhuān)區(qū)
違法和不良信息舉報(bào)電話(huà):027-86699610 舉報(bào)郵箱:58377363@163.com