
已知函數(shù) .
.
(1)若存在 ,使不等式
,使不等式 成立,求實數(shù)
成立,求實數(shù) 的取值范圍;
的取值范圍;
(2)設(shè) ,證明:
,證明: .
.
(1)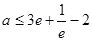 ;(2)詳見解析.
;(2)詳見解析.
解析試題分析:(1)這是一個含參不等式恒成立,求參數(shù)取值范圍的問題,通常方法是根據(jù)函數(shù)性質(zhì)進行求解,或分離參數(shù)轉(zhuǎn)化為求函數(shù)最值問題,若方便分離參數(shù)又較容易求分離后函數(shù)的最值,還是分離參數(shù)較好,這樣可避免對參數(shù)的討論;(2)這是一個以函數(shù)的凹凸那條性為背景的一個不等式的證明問題雙變元問題,可以將其中一個看成主元,另一個看成參數(shù),構(gòu)造函數(shù) ,通過求導判斷函數(shù)的單調(diào)性和最值達到證明的目的.
,通過求導判斷函數(shù)的單調(diào)性和最值達到證明的目的.
試題解析:(1)(1)由 變形為
變形為 .
.
令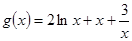 ,則
,則
故當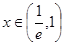 時,
時, ,
, 在
在 上單調(diào)遞減;
上單調(diào)遞減;
當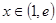 時,
時, ,
, 在
在 上單調(diào)遞增,
上單調(diào)遞增,
所以 的最大值只能在
的最大值只能在 或
或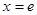 處取得
處取得
又 ,
,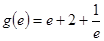 ,所以
,所以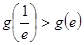
所以 ,從而
,從而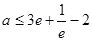 .
.
(2)∵ ,∴
,∴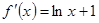
設(shè) ,則
,則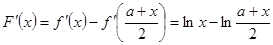
當 時,
時, ,
,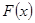 在
在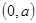 上為減函數(shù);
上為減函數(shù);
當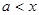 時,
時, ,
,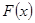 在
在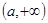 上為增函數(shù).
上為增函數(shù).
從而當 時,
時,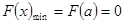 ,
,
因為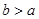 ,所以
,所以 .
.
考點:函數(shù)的零點、三角函數(shù)的性質(zhì).


 世紀百通主體課堂小學課時同步達標系列答案
世紀百通主體課堂小學課時同步達標系列答案 世紀百通優(yōu)練測系列答案
世紀百通優(yōu)練測系列答案科目:高中數(shù)學 來源: 題型:解答題
已知函數(shù) ,
, .
.
(1)若 ,是否存在
,是否存在 、
、 ,使
,使 為偶函數(shù),如果存在,請舉例并證明你的結(jié)論,如果不存在,請說明理由;
為偶函數(shù),如果存在,請舉例并證明你的結(jié)論,如果不存在,請說明理由;
(2)若 ,
, ,求
,求 在
在 上的單調(diào)區(qū)間;
上的單調(diào)區(qū)間;
(3)已知 ,
, 對
對 ,,有
,,有 成立,求
成立,求 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:解答題
已知函數(shù) ,
, 恒過定點 (3,2).
恒過定點 (3,2).
(1)求實數(shù)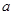 ;
;
(2)在(1)的條件下,將函數(shù) 的圖象向下平移1個單位,再向左平移
的圖象向下平移1個單位,再向左平移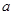 個單位后得到函數(shù)
個單位后得到函數(shù) ,設(shè)函數(shù)
,設(shè)函數(shù) 的反函數(shù)為
的反函數(shù)為 ,求
,求 的解析式;
的解析式;
(3)對于定義在[1,9]的函數(shù) ,若在其定義域內(nèi),不等式
,若在其定義域內(nèi),不等式 恒成立,求
恒成立,求 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:解答題
統(tǒng)計表明,某種型號的汽車在勻速行駛中每小時的耗油量y(升)關(guān)于行駛速度x(千米/小時)的函數(shù)解析式可以表示為: .已知甲、乙兩地相距100千米.
.已知甲、乙兩地相距100千米.
(I)當汽車以40千米/小時的速度勻速行駛時,從甲地到乙地要耗油多少升?
(Ⅱ)當汽車以多大的速度勻速行駛時,從甲地到乙地耗油最少?最少為多少升?
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:解答題
已知函數(shù) .
.
(1)當 時,畫出函數(shù)
時,畫出函數(shù) 的簡圖,并指出
的簡圖,并指出 的單調(diào)遞減區(qū)間;
的單調(diào)遞減區(qū)間;
(2)若函數(shù) 有4個零點,求a的取值范圍.
有4個零點,求a的取值范圍.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:解答題
已知函數(shù) (其中
(其中 )的圖象如圖所示.
)的圖象如圖所示.
(1) 求函數(shù) 的解析式;
的解析式;
(2) 設(shè)函數(shù) ,且
,且 ,求
,求 的單調(diào)區(qū)間.
的單調(diào)區(qū)間.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:解答題
對于函數(shù) ,若在定義域內(nèi)存在實數(shù)
,若在定義域內(nèi)存在實數(shù) ,滿足
,滿足 ,則稱
,則稱 為“局部奇函數(shù)”.
為“局部奇函數(shù)”.
(Ⅰ)已知二次函數(shù) ,試判斷
,試判斷 是否為“局部奇函數(shù)”?并說明理由;
是否為“局部奇函數(shù)”?并說明理由;
(Ⅱ)若 是定義在區(qū)間
是定義在區(qū)間 上的“局部奇函數(shù)”,求實數(shù)
上的“局部奇函數(shù)”,求實數(shù) 的取值范圍;
的取值范圍;
(Ⅲ)若 為定義域
為定義域 上的“局部奇函數(shù)”,求實數(shù)
上的“局部奇函數(shù)”,求實數(shù) 的取值范圍.
的取值范圍.
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com