
【題目】已知函數f(x)=2sin(ωx+φ)(ω>0,|φ|< ![]() )的圖象過點B(0,﹣1),且在(
)的圖象過點B(0,﹣1),且在( ![]() ,
, ![]() )上單調,同時f(x)的圖象向左平移π個單位之后與原來的圖象重合,當x1 , x2∈(﹣
)上單調,同時f(x)的圖象向左平移π個單位之后與原來的圖象重合,當x1 , x2∈(﹣ ![]() ,﹣
,﹣ ![]() ),且x1≠x2時,f(x1)=f(x2),則f(x1+x2)=( )
),且x1≠x2時,f(x1)=f(x2),則f(x1+x2)=( )
A.﹣ ![]()
B.﹣1
C.1
D.![]()
【答案】B
【解析】解:由函數f(x)=2sin(ωx+φ)的圖象過點B(0,﹣1),
∴2sinφ=﹣1,解得sinφ=﹣ ![]() ,
,
又|φ|< ![]() ,∴φ=﹣
,∴φ=﹣ ![]() ,
,
∴f(x)=2sin(ωx﹣ ![]() );
);
又f(x)的圖象向左平移π個單位之后為
g(x)=2sin[ω(x+π)﹣ ![]() ]=2sin(ωx+ωπ﹣
]=2sin(ωx+ωπ﹣ ![]() ),
),
由兩函數圖象完全重合知ωπ=2kπ,∴ω=2k,k∈Z;
又 ![]() ﹣
﹣ ![]() ≤
≤ ![]() =
= ![]() ,
,
∴ω≤ ![]() ,∴ω=2;
,∴ω=2;
∴f(x)=2sin(2x﹣ ![]() ),其圖象的對稱軸為x=
),其圖象的對稱軸為x= ![]() +
+ ![]() ,k∈Z;
,k∈Z;
當x1,x2∈(﹣ ![]() ,﹣
,﹣ ![]() ),其對稱軸為x=﹣3×
),其對稱軸為x=﹣3× ![]() +
+ ![]() =﹣
=﹣ ![]() ,
,
∴x1+x2=2×(﹣ ![]() )=﹣
)=﹣ ![]() ,
,
∴f(x1+x2)=f(﹣ ![]() )
)
=2sin[2×(﹣ ![]() )﹣
)﹣ ![]() ]
]
=2sin(﹣ ![]() )
)
=﹣2sin ![]()
=﹣2sin ![]() =﹣1.
=﹣1.
應選:B.
【考點精析】掌握函數y=Asin(ωx+φ)的圖象變換是解答本題的根本,需要知道圖象上所有點向左(右)平移![]() 個單位長度,得到函數
個單位長度,得到函數![]() 的圖象;再將函數
的圖象;再將函數![]() 的圖象上所有點的橫坐標伸長(縮短)到原來的
的圖象上所有點的橫坐標伸長(縮短)到原來的![]() 倍(縱坐標不變),得到函數
倍(縱坐標不變),得到函數![]() 的圖象;再將函數
的圖象;再將函數![]() 的圖象上所有點的縱坐標伸長(縮短)到原來的
的圖象上所有點的縱坐標伸長(縮短)到原來的![]() 倍(橫坐標不變),得到函數
倍(橫坐標不變),得到函數![]() 的圖象.
的圖象.


科目:高中數學 來源: 題型:
【題目】已知:函數![]() 對一切實數
對一切實數![]() ,
,![]() 都有
都有![]() 成立,且
成立,且![]() .
.
(![]() )求
)求![]() 的值.
的值.
(![]() )求
)求![]() 的解析式.
的解析式.
(![]() )已知
)已知![]() ,設
,設![]() 當
當![]() 時,不等式
時,不等式![]() 恒成立,
恒成立, ![]() 當
當![]() 時,
時,![]() 是單調函數,如果滿足
是單調函數,如果滿足![]() 成立的
成立的![]() 的集合記為
的集合記為![]() ,滿足
,滿足![]() 成立的
成立的![]() 的集合記為
的集合記為![]() ,求
,求![]() (
(![]() 為全集).
為全集).
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】將參加夏令營的600名學生編號為:001,002,…,600,采用系統抽樣的方法抽取一個容量為50的樣本,且隨機抽得的編號為003.這600名學生分住在3個營區,從001到300住在第1營區,從301到495住在第2營區,從496到600住在第3營區,則3個營區被抽中的人數依次為( )
A. 26,16,8 B. 25,16,9
C. 25,17,8 D. 24,17,9
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在三棱柱ABC﹣A1B1C1中,底面△ABC是等邊三角形,側面AA1B1B為正方形,且AA1⊥平面ABC,D為線段AB上的一點. 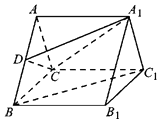
(Ⅰ)若BC1∥平面A1CD,確定D的位置,并說明理由;
(Ⅱ)在(Ⅰ)的條件下,求二面角A1D﹣C﹣BC1的余弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=|x+a|.
(1)若a=2,解關于x的不等式f(x)+f(x﹣3)≥5;
(2)若關于x的不等式f(x)﹣f(x+2)+4≥|1﹣3m|恒成立,求實數m的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,已知三棱柱![]() 的所有棱長都相等,且側棱垂直于底面,由
的所有棱長都相等,且側棱垂直于底面,由![]() 沿棱柱側面經過棱
沿棱柱側面經過棱![]() 到點
到點![]() 的最短路線長為
的最短路線長為![]() ,設這條最短路線與
,設這條最短路線與![]() 的交點為
的交點為![]() .
.
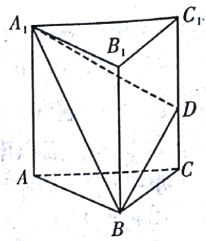
(1)求三棱柱![]() 的體積;
的體積;
(2)證明:平面![]() 平面
平面![]() .
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com