【題目】設函數
，曲線
在點
處的切線與直線
垂直（其中
為自然對數的底數）。
（Ⅰ）若
在區間
上存在極值，求實數
的取值范圍；
（Ⅱ）求證：當
時，不等式
。
【答案】（Ⅰ）
；（Ⅱ）證明見解析；
【解析】試題分析：（1）首先利用切線的斜率建立方程，求出
；利用導數求得函數的極值點，極值點介于
之間，由此求得
的取值范圍；（2）先用分析法，將原不等式等價變形為
，利用導數求出左邊函數的最小值和右邊函數的最大值即可證得原不等式成立.
試題解析：
（1） 因為
，所以
又據題意，得
，所以
，所以
所以
，
所以
當
時，
，
為增函數；
當
時，
，為減函數.
所以函數僅當
時，取得極值
又函數在區間
上存在極值，所以
，所以
.
故實數的取值范圍是
（2）當
時，
，即為.
令
，則
.
再令
，則
.
又因為，所以
.
所以
在
上是增函數.
又因為
.
所以當時，
.
所以
在區間上是增函數.
所以當時，
，又
，故
令
，則
.
因為，所以
.
所以當時，
.故函數
在區間上是減函數.
又
，
所以當時，
，
所以
，即
.
科目：高中數學 來源： 題型：
【題目】如圖，在直三棱柱ABC﹣A1B1C1中，AB⊥AC，AB=BB1=1，B1C=2．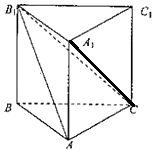 
（1）求證：平面B1AC⊥平面ABB1A1；
（2）求直線A1C與平面B1AC所成角的正弦值．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數f（x）=ax2﹣4ax+b（a＞0）在區間[0，1]上有最大值1和最小值﹣2．
（1）求a，b的值；
（2）若不等式f（x）≥mx在x∈（0，+∞）上恒成立，求實數m的取值范圍．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知向量 
=（cosα﹣ 
，﹣1）， 
=（sinα，1）， 與 為共線向量，且α∈[﹣ 
，0]．
（1）求sinα+cosα的值；
（2）求 
的值．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】若an=log（n+1）（n+2）（n∈N），我們把使乘積a1a2…an為整數的數n叫做“劣數”，則在區間（1，2004）內所有劣數的和為 ．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某公司今年年初用25萬元引進一種新的設備，投入設備后每年收益為21萬元．該公司第n年需要付出設備的維修和工人工資等費用an的信息如圖．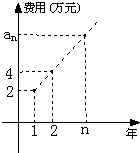 
（1）求an；
（2）引進這種設備后，第幾年后該公司開始獲利；
（3）這種設備使用多少年，該公司的年平均獲利最大？
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖所示，四棱錐P﹣ABCD的底面ABCD是邊長為1的菱形，∠BCD=60°，E是CD的中點，PA⊥底面ABCD，PA=2． （Ⅰ）證明：平面PBE⊥平面PAB；
（Ⅱ）求平面PAD和平面PBE所成二面角（銳角）的余弦值．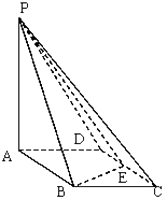
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】以邊長為
的正三角形
的頂點
為坐標原點，另外兩個頂點在拋物線
上，過拋物線
的焦點
的直線
過交拋物線
于
兩點.
（1）求拋物線
的方程；
（2）求證： 
為定值；
（3）求線段
的中點的軌跡方程.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
