
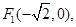
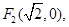 滿足條件
滿足條件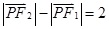 的點P的軌跡是曲線E,直線
的點P的軌跡是曲線E,直線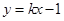 與曲線E交于A、B兩點。如果
與曲線E交于A、B兩點。如果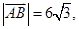 且曲線E上存在點C,使
且曲線E上存在點C,使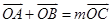 .
.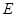 的方程;
的方程;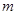 的值.
的值.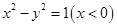 ;(Ⅱ)
;(Ⅱ)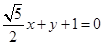 。(Ⅲ)
。(Ⅲ)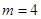 。
。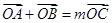 ,得到坐標關系式,結合上一問的結論,可知參數m的等式,得到結論。
,得到坐標關系式,結合上一問的結論,可知參數m的等式,得到結論。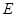 是以
是以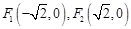 為焦點的雙曲線的左支,且
為焦點的雙曲線的左支,且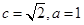 ,易知
,易知
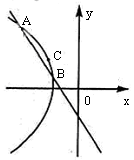
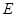 的方程為
的方程為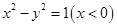 ……….4分
……….4分 ,由題意建立方程組
,由題意建立方程組
 ,得
,得
 ,有
,有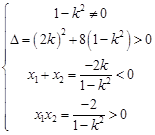 解得
解得
 ……….6分
……….6分

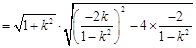
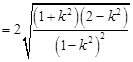
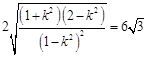 整理后得
整理后得 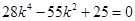
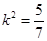 或
或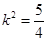 但
但 ∴
∴
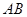 的方程為
的方程為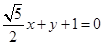 ……….9分
……….9分 ,由已知
,由已知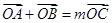 ,得
,得
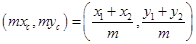 ,
,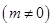
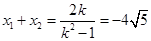 ,
,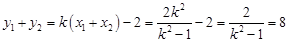
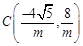 將點
將點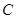 的坐標代入曲線
的坐標代入曲線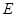 的方程,得
的方程,得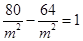
 ,但當
,但當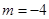 時,所得的點在雙曲線的右支上,不合題意 ∴
時,所得的點在雙曲線的右支上,不合題意 ∴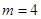 ,…13分
,…13分

科目:高中數學 來源:不詳 題型:單選題
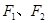 為雙曲線
為雙曲線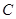 :
: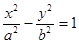 (
(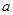 >0,b>0)的焦點,
>0,b>0)的焦點,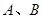 分別為雙曲線的左右頂點,以
分別為雙曲線的左右頂點,以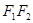 為直徑的圓與雙曲線的漸近線在第一象限的交點為
為直徑的圓與雙曲線的漸近線在第一象限的交點為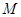 ,且滿足
,且滿足 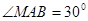 ,則該雙曲線的離心率為
,則該雙曲線的離心率為| A.2 | B.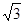 | C.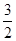 | D.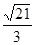 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com