
���}Ŀ������С�}�M�֞�16�����O(sh��)A��B�քe��E�A![]()
![]() ��������c(di��n)���E�A���L(zh��ng)�S�L(zh��ng)��
��������c(di��n)���E�A���L(zh��ng)�S�L(zh��ng)��![]() �����c(di��n)
�����c(di��n)![]() ��ԓ�E�A�ϣ�
��ԓ�E�A�ϣ�
��1����E�A�ķ��̣�
��2���O(sh��)![]() ��ֱ��
��ֱ��![]() �ϲ�ͬ���c(di��n)
�ϲ�ͬ���c(di��n)![]() ������һ�c(di��n)����ֱ��
������һ�c(di��n)����ֱ��![]() �c�E�A�ཻ�ڮ���
�c�E�A�ཻ�ڮ���![]() ���c(di��n)
���c(di��n)![]() ���C������
���C������![]() ���g��������
���g��������
���𰸡���1��![]() ��2��ԔҊ����
��2��ԔҊ����
��������
ԇ�}��������1����E�A�ķ���һ�����ô���ϵ��(sh��)����⣬���}�ɂ�(g��)��(d��)���l������������Ѓɂ�(g��)δ֪��(sh��)���P(gu��n)�I�L(zh��ng)�S�L(zh��ng)��![]() �ėl���������e(cu��)����2���C����
�ėl���������e(cu��)����2���C����![]() ���g����������������������(sh��)���e���C��
���g����������������������(sh��)���e���C��![]() ���@��ֻ���г����c(di��n)����(bi��o)����.
���@��ֻ���г����c(di��n)����(bi��o)����.
ԇ�}��������1�����}�⣺![]() ������
������![]() ������E�A���̞�
������E�A���̞�![]() ��
��
���c(di��n)![]() �ڙE�A�ϣ��ɵ�
�ڙE�A�ϣ��ɵ�![]() ������E�A���̞�
������E�A���̞�![]() ��
��
��2���C��������1��֪��![]() ���O(sh��)
���O(sh��)![]() ��
��![]() ��
��
�tֱ��![]() �ķ��̞飺
�ķ��̞飺![]() ��
��
��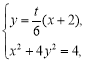 ��
��![]() ��
��
��?y��n)�ֱ��![]() �c�E�A�ཻ�ڮ���
�c�E�A�ཻ�ڮ���![]() ���c(di��n)
���c(di��n)![]() ��
��
����![]() ������
������![]() ��
��
��![]() ����
����![]() ������
������![]() ��
��
�Ķ�![]() ��
��![]() ��
��
����![]()
![]() ��
��
��![]() ���c(di��n)������������
���c(di��n)������������![]() ���g�ǣ�
���g�ǣ�
������![]() ���g��������
���g��������


 ��������ؑc������ϵ�д�
��������ؑc������ϵ�д�
| �꼉(j��) | �����n�� | �꼉(j��) | �����n�� |
| ��һ | ��һ���M(f��i)�n�����]�� | ��һ | ��һ���M(f��i)�n�����]�� |
| �߶� | �߶����M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
| ���� | �������M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ����2017�ؑc���\����֪����(sh��)![]() ���O(sh��)�P(gu��n)��
���O(sh��)�P(gu��n)��![]() �ķ���
�ķ���![]() ��
��![]() ��(g��)��ͬ�Č�(sh��)��(sh��)�⣬�t
��(g��)��ͬ�Č�(sh��)��(sh��)�⣬�t![]() �����п��ܵ�ֵ�飨 ��
�����п��ܵ�ֵ�飨 ��
A�� 3 B�� 1��3 C�� 4��6 D�� 3��4��6
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ����֪����(sh��)f��x��=Asin����x+�գ�+B��A��0���أ�0����һϵ�Ќ�(du��)��(y��ng)ֵ�����
x | �� |
|
|
|
|
|
|
y | ��1 | 1 | 3 | 1 | ��1 | 1 | 3 |
��1������(j��)�����ṩ�Ĕ�(sh��)��(j��)��(sh��)f��x����һ��(g��)����ʽ��
��2������(j��)��1���ĽY(ji��)����
�� i����(d��ng)x��[0�� ![]() ]�r(sh��)������f��3x��=mǡ�Ѓɂ�(g��)��ͬ�Ľ⣬��(sh��)��(sh��)m��ȡֵ������
]�r(sh��)������f��3x��=mǡ�Ѓɂ�(g��)��ͬ�Ľ⣬��(sh��)��(sh��)m��ȡֵ������
�� ii�������������J�������εăɂ�(g��)��(n��i)�ǣ�ԇ���^f��sin�����cf��cos�£��Ĵ�С��
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ����֪�c(di��n)A�� ![]() +1��0����B��0��2������ֱ��l��y=k��x��1��+1�c����AB�ཻ���tֱ��l�Aб�Ǧ���ȡֵ�����ǣ� ��
+1��0����B��0��2������ֱ��l��y=k��x��1��+1�c����AB�ཻ���tֱ��l�Aб�Ǧ���ȡֵ�����ǣ� ��
A.[ ![]() ��
�� ![]() ]
]
B.[0�� ![]() ]
]
C.[0�� ![]() ]��[
]��[ ![]() ����
����
D.[ ![]() ����
����
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ����֪����(sh��)f��x��= ![]() ��2ax+1+lnx
��2ax+1+lnx
��1����(d��ng)a=0�r(sh��)��������(sh��)f��x������D��������һ�c(di��n)A̎���о�б�ʞ�k����k����Сֵ������˕r(sh��)���о����̣�
��2��������(sh��)f��x���ĘO��ֵ�c(di��n)��x1 �� �C����x1lnx1��ax12����1��
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ����ֱ֪������ABCD��A1B1C1D1�У�����ABCD�������Σ�AA1=2AB��E��AA1�����c(di��n)���t����ֱ��BE�cCD1���ɽǵ�����ֵ�飨 ��
A.![]()
B.![]()
C.![]()
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ������С�}�M��16�֣���ƽ��ֱ������(bi��o)ϵ![]() �У���֪�E�A
�У���֪�E�A![]() ��
�� ![]() ���x����
���x����![]() ��ֱ��
��ֱ��![]() �^(gu��)�E�A
�^(gu��)�E�A![]() ���ҽ��c(di��n)
���ҽ��c(di��n)![]() ���ҽ��E�A
���ҽ��E�A![]() ��
��![]() ��
�� ![]() ���c(di��n)��
���c(di��n)��
��1����E�A![]() �Ę�(bi��o)��(zh��n)���̣�
�Ę�(bi��o)��(zh��n)���̣�
��2����֪�c(di��n)![]() ���B�Y(ji��)
���B�Y(ji��)![]() ���^(gu��)�c(di��n)
���^(gu��)�c(di��n)![]() ����ֱ��
����ֱ��![]() �S��ֱ��
�S��ֱ��![]() ���O(sh��)ֱ��
���O(sh��)ֱ��![]() �cֱ��
�cֱ��![]() �����c(di��n)
�����c(di��n)![]() ��ԇ̽����(d��ng)
��ԇ̽����(d��ng)![]() ׃���r(sh��)���Ƿ����һ�l��ֱ��
׃���r(sh��)���Ƿ����һ�l��ֱ��![]() ��ʹ���c(di��n)
��ʹ���c(di��n)![]() ����ֱ��
����ֱ��![]() �ϣ������ڣ�Ո(q��ng)���ֱ��
�ϣ������ڣ�Ո(q��ng)���ֱ��![]() �ķ��̣��������ڣ�Ո(q��ng)�f(shu��)�����ɣ�
�ķ��̣��������ڣ�Ո(q��ng)�f(shu��)�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ�����в���ʽ�н⼯�錍(sh��)��(sh��)��R���ǣ� ��
A.x2+4x+4��0
B.![]()
C.x2��x+1��0
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ�������}�M��16�֣���D����ƽ��ֱ������(bi��o)ϵ![]() �У��x���ʞ�
�У��x���ʞ�![]() �ęE�A
�ęE�A![]()
![]() ������c(di��n)��
������c(di��n)��![]() ���^(gu��)ԭ�c(di��n)
���^(gu��)ԭ�c(di��n)![]() ��ֱ�����c����(bi��o)�S���غϣ��c�E�A
��ֱ�����c����(bi��o)�S���غϣ��c�E�A![]() ����
����![]() ���c(di��n)��ֱ��
���c(di��n)��ֱ��![]() �քe�c
�քe�c![]() �S����
�S����![]() ���c(di��n)����ֱ��
���c(di��n)����ֱ��![]() б�ʞ�
б�ʞ�![]() �r(sh��)��
�r(sh��)�� ![]() ��
��

��1����E�A![]() �Ę�(bi��o)��(zh��n)���̣�
�Ę�(bi��o)��(zh��n)���̣�
��2��ԇ��(w��n)��![]() ��ֱ���ĈA�Ƿ�(j��ng)�^(gu��)���c(di��n)���cֱ��
��ֱ���ĈA�Ƿ�(j��ng)�^(gu��)���c(di��n)���cֱ��![]() ��б�ʟo(w��)�P(gu��n)����Ո(q��ng)�C����ĽY(ji��)Փ��
��б�ʟo(w��)�P(gu��n)����Ո(q��ng)�C����ĽY(ji��)Փ��
�鿴�𰸺ͽ���>>
��(gu��)�H�W(xu��)У��(y��u)�x - ����(x��)��(c��)�б� - ԇ�}�б�
����ʡ��(li��n)�W(w��ng)�`���Ͳ�����Ϣ�e��(b��o)ƽ�_(t��i) | �W(w��ng)���к���Ϣ�e��(b��o)���^(q��) | ����p�_�e��(b��o)���^(q��) | ��vʷ̓�o(w��)���x�к���Ϣ�e��(b��o)���^(q��) | �����֙�(qu��n)�e��(b��o)���^(q��)
�`���Ͳ�����Ϣ�e��(b��o)�Ԓ��027-86699610 �e��(b��o)�]�䣺58377363@163.com