
【題目】已知橢圓![]() 上的點到它的兩個焦的距離之和為
上的點到它的兩個焦的距離之和為![]() ,以橢圓
,以橢圓![]() 的短軸為直徑的圓
的短軸為直徑的圓![]() 經過這兩個焦點,點
經過這兩個焦點,點![]() ,
, ![]() 分別是橢圓
分別是橢圓![]() 的左、右頂點.
的左、右頂點.
(![]() )求圓
)求圓![]() 和橢圓
和橢圓![]() 的方程.
的方程.
(![]() )已知
)已知![]() ,
, ![]() 分別是橢圓
分別是橢圓![]() 和圓
和圓![]() 上的動點(
上的動點(![]() ,
, ![]() 位于
位于![]() 軸兩側),且直線
軸兩側),且直線![]() 與
與![]() 軸平行,直線
軸平行,直線![]() ,
, ![]() 分別與
分別與![]() 軸交于點
軸交于點![]() ,
, ![]() .求證:
.求證: ![]() 為定值.
為定值.
 輕松暑假總復習系列答案
輕松暑假總復習系列答案科目:高中數學 來源: 題型:
【題目】下列說法錯誤的是( )
A.若a,b∈R,且a+b>4,則a,b至少有一個大于2
B.若p是q的充分不必要條件,則¬p是¬q的必要不充分條件
C.若命題p:“ ![]() >0”,則¬p:“
>0”,則¬p:“ ![]() ≤0”
≤0”
D.△ABC中,A是最大角,則sin2A>sin2B+sin2C是△ABC為鈍角三角形的充要條件
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系中,O為坐標原點,A,B,C三點滿足![]() 。
。
(1)求證:A,B,C三點共線;
(2)若A(1,cosx),B(1+sinx,cosx),且x∈[0, ![]() ],函數f(x)=
],函數f(x)=![]() (2m+
(2m+![]() )|
)|![]() |+m2的最小值為5,求實數m的值。
|+m2的最小值為5,求實數m的值。
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】太原五中是一所有著百年歷史的名校,圖1是某一階段來我校參觀學習的外校人數統計莖葉圖,第1次到第14次參觀學習人數依次記為A1 , A2 , …,A14 , 圖2是統計莖葉圖中人數在一定范圍內的一個算法流程圖,那么算法流程圖輸出的結果是 . 
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知數列{an}滿足: ![]() ,anan+1<0(n≥1),數列{bn}滿足:bn=an+12﹣an2(n≥1).
,anan+1<0(n≥1),數列{bn}滿足:bn=an+12﹣an2(n≥1).
(1)求數列{an},{bn}的通項公式
(2)證明:數列{bn}中的任意三項不可能成等差數列.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖所示,在四棱柱ABCD﹣A1B1C1D1中,底面ABCD是梯形,AD∥BC,側面ABB1A1為菱形,∠DAB=∠DAA1 . 
(1)求證:A1B⊥AD;
(2)若AD=AB=2BC,∠A1AB=60°,點D在平面ABB1A1上的射影恰為線段A1B的中點,求平面DCC1D1與平面ABB1A1所成銳二面角的余弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】貴陽與凱里兩地相距約200千米,一輛貨車從貴陽勻速行駛到凱里,規定速度不得超過100千米![]() 時,已知貨車每小時的運輸成本
時,已知貨車每小時的運輸成本![]() 以元為單位
以元為單位![]() 由可變部分和固定部分組成:可變部分與速度
由可變部分和固定部分組成:可變部分與速度![]() 千米
千米![]() 時
時![]() 的平方成正比,比例系數為
的平方成正比,比例系數為![]() ;固定部分為64元.
;固定部分為64元.
![]() 把全程運輸成本
把全程運輸成本![]() 元
元![]() 表示為速度
表示為速度![]() 千米
千米![]() 時
時![]() 的函數,并指出這個函數的定義域;
的函數,并指出這個函數的定義域;
![]() 為了使全程運輸成本最小,貨車應以多大速度行駛?
為了使全程運輸成本最小,貨車應以多大速度行駛?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】心理學家發現視覺和空間能力與性別有關,孝感市黃陂路高中數學興趣小組為了驗證這個結論,從興趣小組中抽取50名同學(男30女20),給所有同學幾何題和代數題各一題,讓各位同學自由選擇一道題進行解答.選題情況如下表:(單位:人)

(1)能否據此判斷有![]() 的把握認為視覺和空間能力與性別有關?
的把握認為視覺和空間能力與性別有關?
(2)以上列聯表中女生選做幾何題的頻率作為概率,從該校1500名女生中隨機選6名女生,記6名女生選做幾何題的人數為![]() ,求
,求![]() 的數學期望
的數學期望![]() 和方差
和方差![]() .
.
附表:

參考公式: 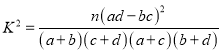 ,其中
,其中![]() .
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com