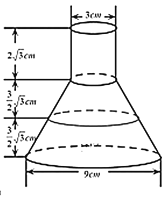
【題目】《烏鴉喝水》是《伊索寓言》中一個寓言故事，通過講述已知烏鴉喝水的故事，告訴人們遇到困難要運用智慧，認真思考才能讓問題迎刃而解的道理，如圖
所示，烏鴉想喝水，發現有一個錐形瓶，上面部分是圓柱體，下面部分是圓臺，瓶口直徑為
厘米，瓶底直徑為
厘米，瓶口距瓶頸為
厘米，瓶頸到水位線距離和水位線到瓶底距離均為
厘米，現將
顆石子投入瓶中，發現水位線上移
厘米，若只有當水位線到達瓶口時烏鴉才能喝到水，則烏鴉共需要投入的石子數量至少是（ ）
A.顆B.顆C.
顆D.
顆
科目：高中數學 來源： 題型：
【題目】某企業采用新工藝，把企業生產中排放的二氧化碳轉化為一種可利用的化工產品.已知該單位每月的處理量最少為
噸，最多為
噸，月處理成本
（元）與月處理量
（噸）之間的函數關系可近似地表示為
，且每處理一噸二氧化碳得到可利用的化工產品價值為
元.
（1）該單位每月處理量為多少噸時，才能使每噸的平均處理成本最低？
（2）該單位每月能否獲利？如果獲利，求出最大利潤；如果不獲利，則國家至少需要補貼多少元才能使該單位不虧損？
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】下圖統計了截止到2019年年底中國電動汽車充電樁細分產品占比及保有量情況，關于這5次統計，下列說法正確的是（ ）
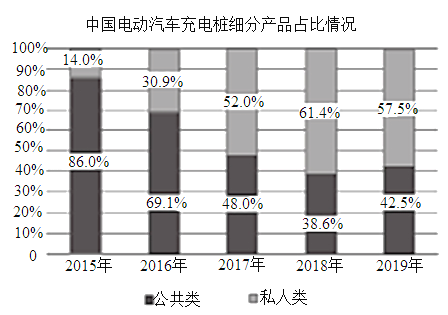
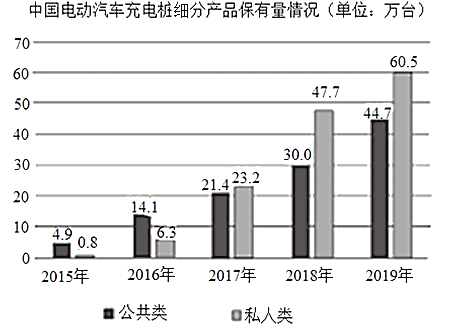
A.私人類電動汽車充電樁保有量增長率最高的年份是2018年
B.公共類電動汽車充電樁保有量的中位數是25.7萬臺
C.公共類電動汽車充電樁保有量的平均數為23.12萬臺
D.從2017年開始，我國私人類電動汽車充電樁占比均超過50%
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】設拋物線C:
與直線
交于A、B兩點.
（1）當
取得最小值為
時，求
的值.
（2）在（1）的條件下，過點
作兩條直線PM、PN分別交拋物線C于M、N（M、N不同于點P）兩點，且
的平分線與
軸平行，求證：直線MN的斜率為定值.
查看答案和解析>>
科目：高中數學 來源： 題型：
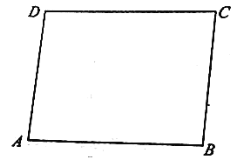
【題目】如圖，矩形
是某生態農莊的一塊植物栽培基地的平面圖，現欲修一條筆直的小路
（寬度不計）經過該矩形區域，其中都在矩形的邊界上.已知
，
（單位：百米），小路將矩形分成面積分別為
，
（單位：平方百米）的兩部分，其中
，且點
在面積為的區域內，記小路的長為
百米.
（1）若
，求的最大值；
（2）若
，求的取值范圍.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】在某地區某高傳染性病毒流行期間，為了建立指標顯示疫情已受控制，以便向該地區居民顯示可以過正常生活，有公共衛生專家建議的指標是“連續7天每天新增感染人數不超過5人”，根據連續7天的新增病例數計算，下列各個選項中，一定符合上述指標的是__________．
①平均數
； ②標準差
； ③平均數且標準差；
④平均數且極差小于或等于2； ⑤眾數等于1且極差小于或等于4.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，在四棱錐VABCD中，底面ABCD是矩形，VD⊥平面ABCD，過AD的平面分別與VB，VC交于點M，N.
(1) 求證：BC⊥平面VCD；
(2) 求證：AD∥MN.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數
(其中
是常數，且
)，曲線
在
處的切線方程為
.
（1）求
的值；
（2）若存在
(其中
是自然對數的底)，使得
成立，求
的取值范圍；
（3）設
，若對任意
，均存在
，使得方程
有三個不同的實數解，求實數
的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
