【題目】已知函數f(x)＝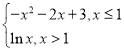
,若關于x的方程f(x)＝kx－
恰有4個不相等的實數根，則實數k的取值范圍是( )
A.
B.
C.
D.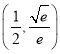
【答案】D
【解析】
由已知可將問題轉化為：y＝f(x)的圖象和直線y＝kx－
有4個交點，作出圖象，由圖可得：點(1,0)必須在直線y＝kx－的下方，即可求得：k＞；再求得直線y＝kx－和y＝ln x相切時，k＝
；結合圖象即可得解.
若關于x的方程f(x)＝kx－恰有4個不相等的實數根，
則y＝f(x)的圖象和直線y＝kx－有4個交點．作出函數y＝f(x)的圖象，如圖，
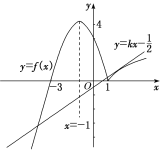
故點(1,0)在直線y＝kx－的下方．
∴k×1－＞0，解得k＞.
當直線y＝kx－和y＝ln x相切時，設切點橫坐標為m，
則k＝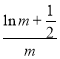
＝
，∴m＝
.
此時，k＝＝，f(x)的圖象和直線y＝kx－有3個交點，不滿足條件，
故所求k的取值范圍是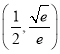
，
故選D..
新課標階梯閱讀訓練系列答案科目：高中數學 來源： 題型：
【題目】如圖，在斜三棱柱ABC﹣A1B1C1中，點O、E分別是A1C1、A1B1的中點，A1C與AC1交于點F，AO⊥平面A1B1C1．已知∠BCA＝90°，AA1＝AC＝BC＝2．
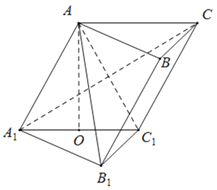
（1）求證：EF∥平面BB1C1C；
（2）求A1C1與平面AA1B1所成角的正弦值．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】在平面直角坐標系
中，曲線
的參數方程為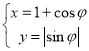
（
為參數）.在以坐標原點為極點，
軸的正半軸為極軸的極坐標系中，直線
的極坐標方程為
.
（1）求曲線的普通方程及直線的直角坐標方程；
（2）求曲線上的點到直線的距離的最大值與最小值.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】2019年11月15日，我市召開全市創建全國文明城市動員大會，會議向全市人民發出動員令，吹響了集結號.為了了解哪些人更關注此活動，某機構隨機抽取了年齡在15～75歲之間的100人進行調查，并按年齡繪制的頻率分布直方圖如圖所示，其分組區間為：
，
，
，
，
，
.把年齡落在
和
內的人分別稱為“青少年人”和“中老年人”，經統計“青少年人”與“中老年人”的人數之比為
.
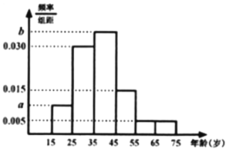
（1）求圖中
的值，若以每個小區間的中點值代替該區間的平均值，估計這100人年齡的平均值
；
（2）若“青少年人”中有15人關注此活動，根據已知條件完成題中的
列聯表，根據此統計結果，問能否有
的把握認為“中老年人”比“青少年人”更加關注此活動？
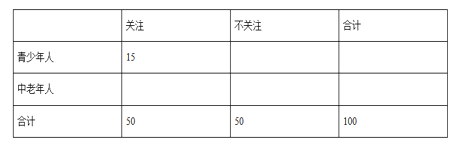
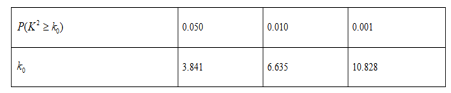
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某企業有甲、乙兩套設備生產同一種產品，為了檢測兩套設備的生產質量情況，隨機從兩套設備生產的大量產品中各抽取了50件產品作為樣本，檢測一項質量指標值，若該項質量指標值落在
內，則為合格品，否則為不合格品. 表1是甲套設備的樣本的頻數分布表，圖1是乙套設備的樣本的頻率分布直方圖.
表1：甲套設備的樣本的頻數分布表
質量指標值 | [95,100) | [100,105) | [105,110) | [110,115) | [115,120) | [120,125] |
頻數 | 1 | 4 | 19 | 20 | 5 | 1 |
圖1：乙套設備的樣本的頻率分布直方圖
（1）填寫下面列聯表，并根據列聯表判斷是否有90%的把握認為該企業生產的這種產品的質量指標值與甲、乙兩套設備的選擇有關；
