
【題目】為了解某社區居民的家庭年收入與年支出的關系,相關部門隨機調查了該社區5戶家庭,得到如表統計數據表:
收入x(萬元) | 8.2 | 8.6 | 10.0 | 11.3 | 11.9 |
支出y(萬元) | 6.2 | 7.5 | 8.0 | 8.5 | 9.8 |
(1)根據上表可得回歸直線方程 ![]() =
= ![]() x+
x+ ![]() ,其中
,其中 ![]() =0.76,
=0.76, ![]() =
= ![]() ﹣
﹣ ![]()
![]() ,據此估計,該社區一戶年收入為15萬元的家庭年支出為多少?
,據此估計,該社區一戶年收入為15萬元的家庭年支出為多少?
(2)若從這5個家庭中隨機抽選2個家庭進行訪談,求抽到家庭的年收入恰好一個不超過10萬元,另一個超過11萬元的概率.
 名校課堂系列答案
名校課堂系列答案科目:高中數學 來源: 題型:
【題目】某公司對新研發的一種產品進行合理定價,且銷量與單價具有相關關系,將該產品按事先擬定的價格進行試銷,得到如下數據:
單價x(單位:元) | 8 | 8.2 | 8.4 | 8.6 | 8.8 | 9 |
銷量y(單位:萬件) | 90 | 84 | 83 | 80 | 75 | 68 |
(1)現有三條y對x的回歸直線方程: ![]() =﹣10x+170;
=﹣10x+170; ![]() =﹣20x+250;
=﹣20x+250; ![]() =﹣15x+210;根據所學的統計學知識,選擇一條合理的回歸直線,并說明理由.
=﹣15x+210;根據所學的統計學知識,選擇一條合理的回歸直線,并說明理由.
(2)預計在今后的銷售中,銷量與單價服從(1)中選出的回歸直線方程,且該產品的成本是每件5元,為使公司獲得最大利潤,該產品的單價應定多少元?(利潤=銷售收入﹣成本)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖所示,已知點A(1,0),D(﹣1,0),點B,C在單位圓O上,且∠BOC= ![]() .
. 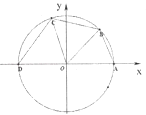
(Ⅰ)若點B( ![]() ,
, ![]() ),求cos∠AOC的值;
),求cos∠AOC的值;
(Ⅱ)設∠AOB=x(0<x< ![]() ),四邊形ABCD的周長為y,將y表示成x的函數,并求出y的最大值.
),四邊形ABCD的周長為y,將y表示成x的函數,并求出y的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下列命題中 ①若loga3>logb3,則a>b;
②函數f(x)=x2﹣2x+3,x∈[0,+∞)的值域為[2,+∞);
③設g(x)是定義在區間[a,b]上的連續函數.若g(a)=g(b)>0,則函數g(x)無零點;
④函數 ![]() 既是奇函數又是減函數.
既是奇函數又是減函數.
其中正確的命題有
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=x2+2bx+c,且f(1)=f(3)=﹣1.設a>0,將函數f(x)的圖像先向右平移a個單位長度,再向下平移a2個單位長度,得到函數g(x)的圖像. (Ⅰ)若函數g(x)有兩個零點x1 , x2 , 且x1<4<x2 , 求實數a的取值范圍;
(Ⅱ)設連續函數在區間[m,n]上的值域為[λ,μ],若有 ![]() ,則稱該函數為“陡峭函數”.若函數g(x)在區間[a,2a]上為“陡峭函數”,求實數a的取值范圍.
,則稱該函數為“陡峭函數”.若函數g(x)在區間[a,2a]上為“陡峭函數”,求實數a的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設函數![]()
(1)討論函數![]() 的單調性;
的單調性;
(2)若![]() 有兩個極值點
有兩個極值點![]() ,記過點
,記過點![]() 的直線的斜率為
的直線的斜率為![]() ,問:是否存在實數
,問:是否存在實數![]() ,使得
,使得![]() ,若存在,求出
,若存在,求出![]() 的值;若不存在,請說明理由.
的值;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知數列{an}是等差數列,若a9+3a11<0,a10a11<0,且數列{an}的前n項和Sn有最大值,那么Sn取得最小正值時n等于( )
A.20
B.17
C.19
D.21
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】用an表示自然數n的所有因數中最大的那個奇數,例如:9的因數有1,3,9,則a9=9;10的因數有1,2,5,10,則a10=5,記數列{an}的前n項和為Sn , 則S ![]() = .
= .
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com