
���}Ŀ��ij��(chu��ng)�F(tu��n)�(du��)�M�_(k��i)�l(f��)һ�N�®a(ch��n)Ʒ������(j��)�Ј�(ch��ng)�{(di��o)���Ӌ(j��)�ܫ@��10�f(w��n)Ԫ��1000�f(w��n)Ԫ�����棬�Ȝ�(zh��n)���ƶ�һ��(g��)��(ji��ng)��(l��)��������(ji��ng)��![]() ����λ���f(w��n)Ԫ���S����
����λ���f(w��n)Ԫ���S����![]() ����λ���f(w��n)Ԫ�������Ӷ����ӣ��Ҫ�(ji��ng)���^(gu��)9�f(w��n)Ԫ��ͬ�r(sh��)��(ji��ng)���^(gu��)�����20%��
����λ���f(w��n)Ԫ�������Ӷ����ӣ��Ҫ�(ji��ng)���^(gu��)9�f(w��n)Ԫ��ͬ�r(sh��)��(ji��ng)���^(gu��)�����20%��
��1������������(sh��)![]() ģ���ƶ���(ji��ng)��(l��)������ԇ�Ô�(sh��)�W(xu��)�Z(y��)�Ա�ʾԓ�F(tu��n)�(du��)��(du��)��(ji��ng)��(l��)����(sh��)
ģ���ƶ���(ji��ng)��(l��)������ԇ�Ô�(sh��)�W(xu��)�Z(y��)�Ա�ʾԓ�F(tu��n)�(du��)��(du��)��(ji��ng)��(l��)����(sh��)![]() ģ�͵Ļ���Ҫ������
ģ�͵Ļ���Ҫ������![]() �Ƿ���ψF(tu��n)�(du��)Ҫ��Ī�(ji��ng)��(l��)����(sh��)ģ�ͣ����f(shu��)��ԭ��
�Ƿ���ψF(tu��n)�(du��)Ҫ��Ī�(ji��ng)��(l��)����(sh��)ģ�ͣ����f(shu��)��ԭ��
��2����ԓ�F(tu��n)�(du��)����ģ�ͺ���(sh��)![]() ���骄(ji��ng)��(l��)����(sh��)ģ�ͣ�ԇ�_����С��������(sh��)
���骄(ji��ng)��(l��)����(sh��)ģ�ͣ�ԇ�_����С��������(sh��)![]() ��ֵ��
��ֵ��
���𰸡���1�������ϣ�Ҋ(ji��n)��������2��328��
��������
��1������(j��)�l���ó�f��x��������(g��)�l�������Д�y![]() 2�Ƿ�M(m��n)��3��(g��)�l����
2�Ƿ�M(m��n)��3��(g��)�l����
��2������(j��)��1��������(g��)�l���в���ʽ���ɴ_��a�ķ������Ķ�����M(m��n)��l������С��������(sh��)a��ֵ��
��1���O(sh��)����(sh��)ģ�͞�![]() ������(j��)�F(tu��n)�(du��)��(du��)����(sh��)ģ�͵Ļ���Ҫ����(sh��)
������(j��)�F(tu��n)�(du��)��(du��)����(sh��)ģ�͵Ļ���Ҫ����(sh��)![]() �M(m��n)�㣺
�M(m��n)�㣺
��(d��ng)![]() �r(sh��)����
�r(sh��)����![]() �ڶ��x��
�ڶ��x��![]() ����������(sh��)����
����������(sh��)����![]() �������
�������
��![]() �������
�������
��(du��)�ں���(sh��)![]() ����(d��ng)
����(d��ng)![]() �r(sh��)��
�r(sh��)��![]() ��������(sh��)��
��������(sh��)��
![]() ������
������![]() �������
�������
��![]() �r(sh��)��
�r(sh��)��![]() ����
����![]() ���������
���������
��ˣ�ԓ����(sh��)ģ�Ͳ����ψF(tu��n)�(du��)Ҫ��
��2����(du��)�ں���(sh��)ģ��![]() ��
��
��(d��ng)![]() ��
��![]() �r(sh��)�f����
�r(sh��)�f����
��(d��ng)![]() �r(sh��)��Ҫʹ
�r(sh��)��Ҫʹ![]() ���������
���������![]() ��
��
����![]() ��
��![]() ��
��
Ҫʹ![]() ���������
���������![]() ��
��![]() �������
�������
�ó�![]() ��
��
�C��������![]() ��
��
���ԝM(m��n)��l������С������(sh��)![]() ��ֵ��328��
��ֵ��328��



| �꼉(j��) | �����n�� | �꼉(j��) | �����n�� |
| ��һ | ��һ���M(f��i)�n�����]�� | ��һ | ��һ���M(f��i)�n�����]�� |
| �߶� | �߶����M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
| ���� | �������M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ����֪![]() �Ƕ��x��
�Ƕ��x��![]() �ϵ�ż����(sh��)���M(m��n)��
�ϵ�ż����(sh��)���M(m��n)��![]() ����(d��ng)
����(d��ng)![]() �r(sh��)��
�r(sh��)��![]() ����
����![]() ��
��![]() ��
��![]() ���t
���t![]() ��
��![]() ��
��![]() �Ĵ�С�P(gu��n)ϵ�飨 ��
�Ĵ�С�P(gu��n)ϵ�飨 ��
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ��ij���Ӱչ����14����ِӰƬ���Mί��(hu��)�փ�����ijһӰԺ��ӳ�@14���Ӱ��ÿ��7����������2��4D�ӰҪ����ͬһ���ӳ�����в���������Ƭ������(sh��)��Ӌ(j��)��ʽ���ǣ� ��
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ���������ļ����غͶ�����ů�r(sh��)�p����Դ�p�ģ����ݵ���픺��≦��Ҫ�������ӡ�ij��������Ҫ�����ʹ��20��ĸ���ӣ�ÿ����ĸ���ӽ���ɱ���6�f(w��n)Ԫ��ԓ������ÿ�����Դ�����M(f��i)��C����λ���f(w��n)Ԫ���c����Ӻ��x����λ��cm���M(m��n)���P(gu��n)ϵ��C��x��=![]() ����������ӣ�ÿ����Դ�����M(f��i)�Þ�8�f(w��n)Ԫ���O(sh��)f��x�������ӽ����M(f��i)���c20�����Դ�����M(f��i)��֮�͡�
����������ӣ�ÿ����Դ�����M(f��i)�Þ�8�f(w��n)Ԫ���O(sh��)f��x�������ӽ����M(f��i)���c20�����Դ�����M(f��i)��֮�͡�
��������k��ֵ��f(x)�ı��_(d��)ʽ��
����������������r(sh��)�����M(f��i)��f(x)�_(d��)����С��������Сֵ��
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ����֪�E�AC��![]() �����ҽ��c(di��n)�քe��
�����ҽ��c(di��n)�քe��![]() ��
��![]() ���x���ʞ�
���x���ʞ�![]() ���c(di��n)
���c(di��n)![]() �ڙE�AC�ϣ���
�ڙE�AC�ϣ���![]() ��
��![]()
![]() ����F1MF2����e��
����F1MF2����e��![]() .
.
(1)��E�AC�Ę�(bi��o)��(zh��n)���̣�
(2)��ֱ֪��(xi��n)l�c�E�AC����A��B���c(di��n)��![]() ����ֱ��(xi��n)lʼ�K�c�A
����ֱ��(xi��n)lʼ�K�c�A![]() ���У���돽r��ֵ.
���У���돽r��ֵ.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ����֪����(sh��)![]() ��
��![]() ����Ȼ��(du��)��(sh��)�ĵה�(sh��)��.
����Ȼ��(du��)��(sh��)�ĵה�(sh��)��.
(1)��(sh��)![]() �ĘOֵ��
�ĘOֵ��
(2)��(w��n)���Ƿ���ڌ�(sh��)��(sh��)![]() ,ʹ��
,ʹ��![]() �Ѓɂ�(g��)�ஐ���c(di��n)��������,���
�Ѓɂ�(g��)�ஐ���c(di��n)��������,���![]() ��ȡֵ��������������,Ո(q��ng)�f(shu��)������.
��ȡֵ��������������,Ո(q��ng)�f(shu��)������.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ����֪?ji��ng)�ֱ��(xi��n)![]() ��ֱ��
��ֱ��![]() �S���c�E�A
�S���c�E�A![]() ����
����![]() ���c(di��n)���c(di��n)
���c(di��n)���c(di��n)![]() ��ֱ��(xi��n)
��ֱ��(xi��n)![]() �ϣ�
�ϣ�![]() .
.
��1�����c(di��n)![]() ��܉�E
��܉�E![]() �ķ��̣�
�ķ��̣�
��2��ֱ��(xi��n)![]() �c�E�A
�c�E�A![]() �ཻ��
�ཻ��![]() ���c����(xi��n)
���c����(xi��n)![]() �������c(di��n)
�������c(di��n)![]() ��
��![]() ������(bi��o)ԭ�c(di��n)����
������(bi��o)ԭ�c(di��n)����![]() ��ȡֵ����.
��ȡֵ����.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ����ƽ��ֱ������(bi��o)ϵ![]() �У���֪���タ(xi��n)
�У���֪���タ(xi��n)![]() �ϵ��c(di��n)
�ϵ��c(di��n)![]() �����c(di��n)
�����c(di��n)![]() �ľ��x��2.
�ľ��x��2.
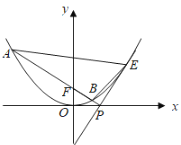
��1�����タ(xi��n)�ķ��̣�
��2����D���c(di��n)![]() �ǒ��タ(xi��n)�Ϯ���ԭ�c(di��n)���c(di��n)�����タ(xi��n)���c(di��n)
�ǒ��タ(xi��n)�Ϯ���ԭ�c(di��n)���c(di��n)�����タ(xi��n)���c(di��n)![]() ̎���о�(xi��n)�c
̎���о�(xi��n)�c![]() �S�ཻ���c(di��n)
�S�ཻ���c(di��n)![]() ��ֱ��(xi��n)
��ֱ��(xi��n)![]() �c���タ(xi��n)�ཻ��
�c���タ(xi��n)�ཻ��![]() ���c(di��n)����
���c(di��n)����![]() ��e����Сֵ��
��e����Сֵ��
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ���������˂����á�ͨ�彛(j��ng)؞��ˇ������һ��(g��)�˲��R(sh��)��ˇ�^(gu��)�ˣ��@��ġ���ˇ���䌍(sh��)Դ���Ї�(gu��)�ܳ����F������wϵ�����w�������Y����(l��)���䡢������(sh��)����(sh��)��.���P(y��ng)�Ї�(gu��)���y(t��ng)�Ļ���ijУ����ĩ�W(xu��)���I(y��)���dȤ���(d��ng)���_(k��i)չ�ˡ���ˇ��֪�R(sh��)�v����ÿˇ����һ��(ji��)���B������(ji��)���t�M(m��n)�㡰��(sh��)���������ǰ�ɹ�(ji��)�����Y���͡���(l��)����횷��_(k��i)���ŵĸ��ʞ飨 ��
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
�鿴�𰸺ͽ���>>
��(gu��)�H�W(xu��)У��(y��u)�x - ����(x��)��(c��)�б� - ԇ�}�б�
����ʡ��(li��n)�W(w��ng)�`���Ͳ�����Ϣ�e��(b��o)ƽ�_(t��i) | �W(w��ng)���к���Ϣ�e��(b��o)��(zhu��n)�^(q��) | ����p�_�e��(b��o)��(zhu��n)�^(q��) | ��vʷ̓�o(w��)���x�к���Ϣ�e��(b��o)��(zhu��n)�^(q��) | �����֙�(qu��n)�e��(b��o)��(zhu��n)�^(q��)
�`���Ͳ�����Ϣ�e��(b��o)�Ԓ(hu��)��027-86699610 �e��(b��o)�]�䣺58377363@163.com