
【題目】在平面直角坐標系![]() 中,已知圓
中,已知圓![]() 的方程是
的方程是![]() .
.
(![]() )如果圓
)如果圓![]() 與直線
與直線![]() 沒有公共點,求實數
沒有公共點,求實數![]() 的取值范圍;
的取值范圍;
(![]() )如果圓
)如果圓![]() 過坐標原點,過點
過坐標原點,過點![]() 直線
直線![]() 與圓
與圓![]() 交于
交于![]() ,
, ![]() 兩點,記直線
兩點,記直線![]() 的斜率的平方為
的斜率的平方為![]() ,對于每一個確定的
,對于每一個確定的![]() ,當
,當![]() 的面積最大時,用含
的面積最大時,用含![]() 的代數式表示
的代數式表示![]() ,并求
,并求![]() 的最大值.
的最大值.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】試題分析:(1)由![]() 可得
可得![]() ,圓
,圓![]() 與直線
與直線![]() 無公共點,
無公共點,
∴![]() ,即
,即![]() ,所以
,所以![]() ;(2)圓
;(2)圓![]() 過坐標原點,可得
過坐標原點,可得![]() ,圓
,圓![]() 方程為
方程為![]() ,圓心
,圓心![]() ,半徑為
,半徑為![]() ,設直線
,設直線![]() 的方程為
的方程為![]() ,∴當
,∴當![]() 最大時,
最大時, ![]() 取最大值.只需點
取最大值.只需點![]() 到直線
到直線![]() 的距離
的距離![]() ,可得
,可得![]() 或
或![]() ,對
,對![]() 討論兩種情況,可得
討論兩種情況,可得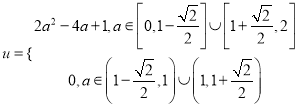 ,兩段分別求出最大值,較大的就是
,兩段分別求出最大值,較大的就是![]() 的最大值
的最大值
試題解析:( ![]() )由
)由![]() 可得
可得![]() ,
,
∵![]() ,表示圓,
,表示圓,
![]() ,即
,即![]() ,
,
又∵圓![]() 與直線
與直線![]() 無公共點,
無公共點,
∴![]() ,即
,即![]() ,
,
綜上, ![]() .
.
(![]() )∵圓
)∵圓![]() 過坐標原點,
過坐標原點,
∴![]() ,圓
,圓![]() 方程為
方程為![]() ,
,
圓心![]() ,半徑為
,半徑為![]() ,
,
當![]() 時,直線
時,直線![]() 經過圓心
經過圓心![]() ,
,
![]() 不存在,故
不存在,故![]() .
.
由題意設直線![]() 的方程為
的方程為![]() ,
,
![]() 的面積為
的面積為![]() ,
,
則![]() ,
,
∴當![]() 最大時,
最大時, ![]() 取最大值.
取最大值.
當![]() ,只需點
,只需點![]() 到直線
到直線![]() 的距離等于
的距離等于![]() ,
,
即![]() .
.
整理得: ![]() ,
,
解出![]() 或
或![]() .
.
①當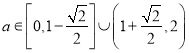 時,
時, ![]() 最大值為
最大值為![]() ,
,
此時![]() ,即
,即![]() .
.
②當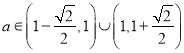 時,
時, ![]() ,
,
∵![]() 是
是![]() 上的減函數,
上的減函數,
∴當![]() 最小時,
最小時, ![]() 最大,
最大,
過![]() 作
作![]() 于
于![]() 點,則
點,則![]() ,
,
∴當![]() 最大時,
最大時, ![]() 最小,
最小,
∵![]() ,且
,且![]() ,
,
∴當![]() 最大時,
最大時, ![]() 取得最大值,即
取得最大值,即![]() 最大,
最大,
∵![]() ,
,
∴當![]() 時,
時, ![]() 取得最大值
取得最大值![]() ,
,
∴當![]() 面積最大時,直線
面積最大時,直線![]() 的斜率
的斜率![]() ,
,
∴![]() ,
,
綜上, 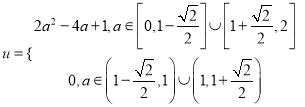 ,
,
∴當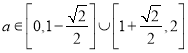 時,
時, ![]() ,
,
當![]() 或
或![]() 時,
時, ![]() 取得最大值
取得最大值![]() ,
,
當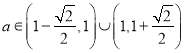 時,
時, ![]() .
.
∴綜上所述, ![]() .
.


 怎樣學好牛津英語系列答案
怎樣學好牛津英語系列答案科目:高中數學 來源: 題型:
【題目】已知一個袋中裝有大小相同的4個紅球,3個白球,3個黃球.若任意取出2個球,則取出的2個球顏色相同的概率是;若有放回地任意取10次,每次取出一個球,每取到一個紅球得2分,取到其它球不得分,則得分數X的方差為 .
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系xOy中,已知橢圓 ![]() +
+ ![]() =1(a>b>0)與雙曲線
=1(a>b>0)與雙曲線 ![]() ﹣y2=1有相同的焦點F1 , F2 , 拋物線x2=2py(p>0)的焦點為F,且與橢圓在第一象限的交點為M,若|MF1|+|MF2|=2
﹣y2=1有相同的焦點F1 , F2 , 拋物線x2=2py(p>0)的焦點為F,且與橢圓在第一象限的交點為M,若|MF1|+|MF2|=2 ![]() .
.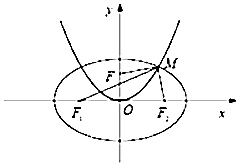
(1)求橢圓的方程;
(2)若|MF|= ![]() ,求拋物線的方程.
,求拋物線的方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】《九章算術》中有“今有五人分無錢,令上二人所得與下三人等,問各得幾何?”.其意思為“已知甲、乙、丙、丁、戊五人分5錢,甲、乙兩人所得與丙、丁、戊三人所得相同,且甲、乙、丙、丁、戊所得依次成等差數列,問五人各得多少錢?”這個問題中,甲所得為( )
A.![]() 錢
錢
B.![]() 錢
錢
C.![]() 錢
錢
D.![]() 錢
錢
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在等差數列{an}中,2a9=a12+13,a2=5,其前n項和為Sn .
(1)求數列{an}的通項公式;
(2)求數列{ ![]() }的前n項和Tn , 并證明Tn<
}的前n項和Tn , 并證明Tn< ![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,△ABC是圓的內接三角形,∠BAC的平分線交圓于點D,交BC于E,過點B的圓的切線與AD的延長線交于點F,在上述條件下,給出下列四個結論:
①BD平分∠CBF;
②FB2=FDFA;
③AECE=BEDE;
④AFBD=ABBF.
所有正確結論的序號是( )
A.①②
B.③④
C.①②③
D.①②④
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知數集![]() 具有性質
具有性質![]() :對任意的
:對任意的![]()
![]() ,
,![]() ,使得
,使得![]() 成立.
成立.
(Ⅰ)分別判斷數集![]() 與
與![]() 是否具有性質
是否具有性質![]() ,并說明理由;
,并說明理由;
(Ⅱ)求證![]() ;
;
(Ⅲ)若![]() ,求數集
,求數集![]() 中所有元素的和的最小值.
中所有元素的和的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知曲線C1 , C2的極坐標方程分別為ρ=2cosθ, ![]() ,射線θ=φ,
,射線θ=φ, ![]() ,
, ![]() 與曲線C1交于(不包括極點O)三點A,B,C.
與曲線C1交于(不包括極點O)三點A,B,C.
(Ⅰ)求證: ![]() ;
;
(Ⅱ)當 ![]() 時,求點B到曲線C2上的點的距離的最小值.
時,求點B到曲線C2上的點的距離的最小值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com