
【題目】已知函數(shù)f(x)=2cos2x+ax2.
(1)當a=1時,求f(x)的導函數(shù)![]() 在
在![]() 上的零點個數(shù);
上的零點個數(shù);
(2)若關(guān)于x的不等式2cos(2sinx)+a2x2≤af(x)在(﹣∞,+∞)上恒成立,求實數(shù)a的取值范圍.
【答案】(1)零點個數(shù)為3;(2)[1,+∞).
【解析】
(1)易得![]() =2(x﹣sin2x),再用導數(shù)法研究(0,
=2(x﹣sin2x),再用導數(shù)法研究(0,![]() )上的零點情況,然后結(jié)合
)上的零點情況,然后結(jié)合![]() 的奇偶性求解.
的奇偶性求解.
(2)令sinx=t∈[﹣1,1],轉(zhuǎn)化為不等式cos2t≤a(1﹣t2)恒成立,再t=±1和﹣1<t<1分類討論求解.
(1)易知![]() =2(x﹣sin2x),顯然
=2(x﹣sin2x),顯然![]() =0,
=0,
所以x=0是f′(x)的一個零點,
令g(x)=x﹣sin2x(0≤x![]() ),則
),則![]() =1﹣2cos2x=0時,x
=1﹣2cos2x=0時,x![]() ,
,
所以g(x)在(0,![]() )單調(diào)遞減,在(
)單調(diào)遞減,在(![]() ,
,![]() )單調(diào)遞增,
)單調(diào)遞增,
則g(x)的最小值為g(![]() )
)![]() 0,
0,
又g(0)=0,且g(![]() )
)![]() 0,
0,
所以g(x)在(0,![]() )上存在唯一零點x0∈(
)上存在唯一零點x0∈(![]() ,
,![]() ),
),
則![]() =2g(x)在(0,
=2g(x)在(0,![]() )上亦存在唯一零點,
)上亦存在唯一零點,
因為![]() 是奇函數(shù),所以
是奇函數(shù),所以![]() 在(
在(![]() ,0)上也存在唯一零點﹣x0,
,0)上也存在唯一零點﹣x0,
綜上所述,當a=1時,f(x)的導函數(shù)![]() 在[
在[![]() ,
,![]() ]上的零點個數(shù)為3;
]上的零點個數(shù)為3;
(2)不等式2cos(2sinx)+a2x2≤af(x)恒成立,即不等式cos(2sinx)≤acos2x恒成立,
令sinx=t∈[﹣1,1],則等價于不等式cos2t≤a(1﹣t2)…(1)恒成立,
①若t2=1,即t=±1時,不等式(1)顯然成立,此時a∈R,
②若﹣1<t<1時,不等式(1)等價于a![]() (2)
(2)
設(shè)h(t)![]() (﹣1<t<1),
(﹣1<t<1),
當0≤t<1時,![]()
 ,
,
令φ(t)=tcos2t﹣(1﹣t2)sin2t(0≤t<1,
則![]() =(2t2﹣1)cos2t(0≤t<1),
=(2t2﹣1)cos2t(0≤t<1),
已知 =0,
=0,![]() =0,且
=0,且![]() ,
,
則φ(t)在(0,![]() ),(
),(![]() ,1)上單調(diào)遞減,在(
,1)上單調(diào)遞減,在(![]() ,
,![]() )上單調(diào)地增,
)上單調(diào)地增,
又φ(0)=0,φ(![]() )=
)=![]() ﹣1<0,所以φ(t)<0在(0,1)上恒成立,
﹣1<0,所以φ(t)<0在(0,1)上恒成立,
所以h(t)在[0,1)上單調(diào)遞減,則h(t)≤h(0)=1,
顯然函數(shù)h(t)為偶函數(shù),故函數(shù)h(t)在[﹣1,1]上的最大值為1,
因此a≥1,
綜上所述,滿足題意的實數(shù)a的取值范圍為[1,+∞).


 閱讀快車系列答案
閱讀快車系列答案科目:高中數(shù)學 來源: 題型:
【題目】對某兩名高三學生在連續(xù)9次數(shù)學測試中的成績(單位:分)進行統(tǒng)計得到折線圖,下面是關(guān)于這兩位同學的數(shù)學成績分析.
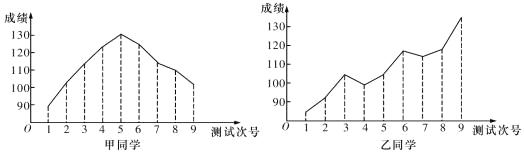
①甲同學的成績折線圖具有較好的對稱性,故平均成績?yōu)?30分;
②根據(jù)甲同學成績折線圖提供的數(shù)據(jù)進行統(tǒng)計,估計該同學平均成績在區(qū)間![]() 內(nèi);
內(nèi);
③乙同學的數(shù)學成績與測試次號具有比較明顯的線性相關(guān)性,且為正相關(guān);
④乙同學連續(xù)九次測驗成績每一次均有明顯進步.
其中正確的個數(shù)為( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】在△ABC中,a,b,c分別為內(nèi)角A,B,C所對邊的邊長,且C=![]() ,a+b=λc(其中λ>1).
,a+b=λc(其中λ>1).
(1)若λ=![]() 時,證明:△ABC為直角三角形;
時,證明:△ABC為直角三角形;
(2)若![]() ·
·![]() =
=![]() λ2,且c=3,求λ的值.
λ2,且c=3,求λ的值.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】甲、乙二人進行一場比賽,該比賽采用三局兩勝制,即先獲得兩局勝利者獲得該場比賽勝利.在每一局比賽中,都不會出現(xiàn)平局,甲獲勝的概率都為![]() .
.
(1)求甲在第一局失利的情況下,反敗為勝的概率;
(2)若![]() ,比賽結(jié)束時,設(shè)甲獲勝局數(shù)為
,比賽結(jié)束時,設(shè)甲獲勝局數(shù)為![]() ,求其分布列和期望
,求其分布列和期望![]() ;
;
(3)若甲獲得該場比賽勝利的概率大于甲每局獲勝的概率,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知點F1、F2分別為雙曲線C:![]() (a>0,b>0)的左、右焦點,點M(x0,y0)(x0<0)為C的漸近線與圓x2+y2=a2的一個交點,O為坐標原點,若直線F1M與C的右支交于點N,且|MN|=|NF2|+|OF2|,則雙曲線C的離心率為_____.
(a>0,b>0)的左、右焦點,點M(x0,y0)(x0<0)為C的漸近線與圓x2+y2=a2的一個交點,O為坐標原點,若直線F1M與C的右支交于點N,且|MN|=|NF2|+|OF2|,則雙曲線C的離心率為_____.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】直線![]() 是過點
是過點![]() 的動直線,當
的動直線,當![]() 與圓
與圓![]() 相切時,同時也和拋物線
相切時,同時也和拋物線![]() 相切.
相切.
(1)求拋物線![]() 的方程;
的方程;
(2)直線![]() 與拋物線
與拋物線![]() 交于不同的兩點
交于不同的兩點![]() ,與圓
,與圓![]() 交于不同的兩點A、B,
交于不同的兩點A、B,![]() 面積為
面積為![]() ,
,![]() 面積為
面積為![]() ,當
,當![]() 時,求直線
時,求直線![]() 的方程.
的方程.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知函數(shù)f(x)![]() ,
,
(1)討論函數(shù)f(x)的單調(diào)性;
(2)證明:a=1時,f(x)+g(x)﹣(1![]() )lnx>e.
)lnx>e.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】《周髀算經(jīng)》中給出了勾股定理的絕妙證明.如圖是趙爽弦圖及注文.弦圖是一個以勾股形之弦為邊的正方形,其面積稱為弦實.圖中包含四個全等的勾股形及一個小正方形,分別涂成朱色及黃色,其面積稱為朱實、黃實.由2×勾×股+(股-勾)2=4×朱實+黃實=弦實,化簡得勾2+股2=弦2.若圖中勾股形的勾股比為![]() ,向弦圖內(nèi)隨機拋擲100顆圖釘(大小忽略不計),則落在黃色圖形內(nèi)的圖釘顆數(shù)大約為( )(參考數(shù)據(jù):
,向弦圖內(nèi)隨機拋擲100顆圖釘(大小忽略不計),則落在黃色圖形內(nèi)的圖釘顆數(shù)大約為( )(參考數(shù)據(jù):![]() ,
,![]() )
)
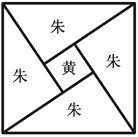
A.2B.4C.6D.8
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com