【題目】甲、乙二人進(jìn)行一場比賽，該比賽采用三局兩勝制，即先獲得兩局勝利者獲得該場比賽勝利.在每一局比賽中，都不會出現(xiàn)平局，甲獲勝的概率都為
.
（1）求甲在第一局失利的情況下，反敗為勝的概率；
（2）若
，比賽結(jié)束時，設(shè)甲獲勝局?jǐn)?shù)為
，求其分布列和期望
；
（3）若甲獲得該場比賽勝利的概率大于甲每局獲勝的概率，求
的取值范圍.
【答案】（1）
；（2）詳見解析；（3）
.
【解析】
（1）設(shè)
甲在第一局失利，
甲獲得了比賽的勝利，利用條件概率的概率公式可求得所求事件的概率；
（2）根據(jù)題意可知隨機(jī)變量
的可能取值為
、
、
，計算出隨機(jī)變量在不同取值下的概率，列出分布列，進(jìn)而可計算出隨機(jī)變量的數(shù)學(xué)期望；
（3）計算出甲獲得該場比賽的概率，根據(jù)題意得出關(guān)于
的不等式，即可解得的取值范圍.
（1）設(shè)甲在第一局失利，甲獲得了比賽的勝利，則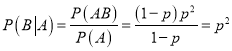
；
（2）由題意可知，隨機(jī)變量的可能取值為、、，
則
，
，
.
隨機(jī)變量的分布列如下：
|
|
|
|
|
|
|
|
則
；
（3）甲獲得該場比賽勝利的概率為
，則
.
即
，解得
，所以的取值范圍是.
教材全解字詞句篇系列答案科目：高中數(shù)學(xué) 來源： 題型：
【題目】在等比數(shù)列
中，已知
設(shè)數(shù)列
的前n項和為
，且
（1）求數(shù)列通項公式；
（2）證明：數(shù)列
是等差數(shù)列；
（3）是否存在等差數(shù)列
，使得對任意
，都有
？若存在，求出所有符合題意的等差數(shù)列；若不存在，請說明理由.
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】已知函數(shù)
，
．
（1）討論函數(shù)
的導(dǎo)函數(shù)
的單調(diào)性；
（2）若函數(shù)在
處取得極大值，求a的取值范圍．
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】某小區(qū)內(nèi)有一塊以
為圓心半徑為20米的圓形區(qū)域.廣場，為豐富市民的業(yè)余文化生活，現(xiàn)提出如下設(shè)計方案：如圖，在圓形區(qū)域內(nèi)搭建露天舞臺，舞臺為扇形
區(qū)域，其中兩個端點
，
分別在圓周上；觀眾席為梯形
內(nèi)且在圓外的區(qū)域，其中
，
，且
，
在點的同側(cè).為保證視聽效果，要求觀眾席內(nèi)每一個觀眾到舞臺處的距離都不超過60米.設(shè)
.
（1）求的長（用
表示）；
（2）對于任意，上述設(shè)計方案是否均能符合要求？
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】人口平均預(yù)期壽命是綜合反映人們健康水平的基本指標(biāo).
年第六次全國人口普查資料表明，隨著我國社會經(jīng)濟(jì)的快速發(fā)展，人民生活水平的不斷提高以及醫(yī)療衛(wèi)生保障體系的逐步完善，我國人口平均預(yù)期壽命繼續(xù)延長，國民整體健康水平有較大幅度的提高.下圖體現(xiàn)了我國平均預(yù)期壽命變化情況，依據(jù)此圖，下列結(jié)論錯誤的是（ ）
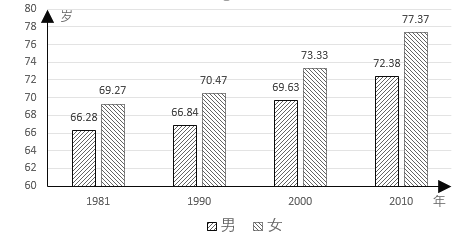
A.男性的平均預(yù)期壽命逐漸延長
B.女性的平均預(yù)期壽命逐漸延長
C.男性的平均預(yù)期壽命延長幅度略高于女性
D.女性的平均預(yù)期壽命延長幅度略高于男性
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】已知定義在R上的函數(shù)
在[1，2]上有且僅有3個零點，其圖象關(guān)于點
和直線x
對稱，給出下列結(jié)論：
①
；
②函數(shù)f（x）在[0，1]上有且僅有3個極值點；
③函數(shù)f（x）在
上單調(diào)遞增；
④函數(shù)f（x）的最小正周期是2．
其中所有正確結(jié)論的編號是（ ）
A.②③B.①④C.②③④D.①②
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】已知函數(shù)f（x）＝2cos2x+ax2．
（1）當(dāng)a＝1時，求f（x）的導(dǎo)函數(shù)
在
上的零點個數(shù)；
（2）若關(guān)于x的不等式2cos（2sinx）+a2x2≤af（x）在（﹣∞，+∞）上恒成立，求實數(shù)a的取值范圍．
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】直線
是過點
的動直線，當(dāng)與圓
相切時，同時也和拋物線
相切.
（1）求拋物線
的方程；
（2）直線與拋物線交于不同的兩點
，與圓
交于不同的兩點A、B，
面積為
，
面積為
，當(dāng)
時，求直線的方程．
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】設(shè)函數(shù)
，已知方程
（
為常數(shù)）在
上恰有三個根，分別為
，下述四個結(jié)論：
①當(dāng)
時，
的取值范圍是
；
②當(dāng)時，
在上恰有2個極小值點和1個極大值點；
③當(dāng)時，在
上單調(diào)遞增；
④當(dāng)
時，的取值范圍為
，且
其中正確的結(jié)論個數(shù)為（ ）
A.1B.2C.3D.4
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
