【題目】“勾股定理”在西方被稱為“畢達哥拉斯定理”，國時期吳國的數學家趙爽創制了一幅“勾股圓方圖”，用數形結合的方法給出了勾股定理的詳細證明
如圖所示的“勾股圓方圖”中，四個相同的直角三角形與中間的小正方形拼成一個大正方形若直角三角形中較小的銳角
，現在向該大止方形區域內隨機地投擲一枚飛鏢，則飛鏢落在陰影部分的概率是
A. 
B. 
C. 
D. 
名校課堂系列答案科目：高中數學 來源： 題型：
【題目】社區服務是高中學生社會實踐活動的一個重要內容，漢中某中學隨機抽取了100名男生、100名女生，了解他們一年參加社區服務的時間，按
，
，
，
，
（單位：小時）進行統計，得出男生參加社區服務時間的頻率分布表和女生參加社區服務時間的頻率分布直方圖.
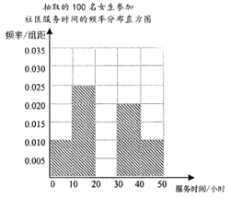
（1）完善男生參加社區服務時間的頻率分布表和女生參加社區服務時間的頻率分布直方圖.
抽取的100名男生參加社區服務時間的頻率分布表
社區服務時間 | 人數 | 頻率 |
| 0.05 | |
| 20 | |
| 0.35 | |
| 30 | |
| ||
合計 | 100 | 1 |
學生社區服務時間合格與性別的列聯表
不合格的人數 | 合格的人數 | |
男 | ||
女 |
（2）按高中綜合素質評價的要求，高中學生每年參加社區服務的時間不少于20個小時才為合格，根據上面的統計圖表，完成抽取的這200名學生參加社區服務時間合格與性別的列聯表，并判斷是否有
以上的把握認為參加社區服務時間達到合格程度與性別有關，并說明理由.
（3）用以上這200名學生參加社區服務的時間估計全市9萬名高中學生參加社區服務時間的情況，并以頻率作為概率.
（i）求全市高中學生參加社區服務時間不少于30個小時的人數.
（ⅱ）對我市高中生參加社區服務的情況進行評價.
參考公式
| 0.150 | 0.100 | 0.050 | 0.025 | 0.010 | 0.002 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
（
，其
）
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】定義向量
的“相伴函數”為
，函數的“相伴向量”為，其中O為坐標原點，記平面內所有向量的“相伴函數”構成的集合為S.
（1）設
，求證：
；
（2）已知
且
，求其“相伴向量”的模；
（3）已知
為圓
上一點，向量
的“相伴函數”
在
處取得最大值，當點M在圓C上運動時，求
的取值范圍.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】今年學雷鋒日，某中學計劃從高中三個年級選派4名教師和若干名學生去當學雷鋒文明交通宣傳志愿者，用分層抽樣法從高中三個年級的相關人員中抽取若干人組成文明交通宣傳小組，學生的選派情況如下：
年級 | 相關人數 | 抽取人數 |
高一 | 99 |
|
高二 | 27 |
|
高三 | 18 | 2 |
（Ⅰ）求
，
的值；
（Ⅱ）若從選派的高一、高二、高三年級學生中抽取3人參加文明交通宣傳，求他們中恰好有1人是高三年級學生的概率；
（Ⅲ）若4名教師可去
、
、
三個學雷鋒文明交通宣傳點進行文明交通宣傳，其中每名教師去、、三個文明交通宣傳點是等可能的，且各位教師的選擇相互獨立.記到文明交通宣傳點的人數為
，求隨機變量的分布列和數學期望.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，在四棱錐S﹣ABCD中，底面ABCD是直角梯形，AB⊥AD，AB⊥BC，側面SAB⊥底面ABCD，且SA＝SB＝AB＝BC＝2，AD＝1．
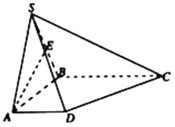
（1）設E為棱SB的中點，求證：AE⊥平面SBC；
（2）求平面SCD與平面SAB所成銳二面角的大小．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
