
【題目】在平面直角坐標系xOy中,已知定點A(-4,0)、C(4,0),半徑為r的圓M的圓心M在線段AC的垂直平分線上,且在y軸右側,圓M被y軸截得的弦長為![]() r.
r.
(1)求圓M的方程;(2)當r變化時,是否存在定直線l與動圓M均相切?如果存在,求出定直線l的方程;如果不存在,說明理由.
【答案】(1)![]() ;(2) 存在兩條直線y=3和4x+3y-9=0與動圓M均相切.
;(2) 存在兩條直線y=3和4x+3y-9=0與動圓M均相切.
【解析】試題分析:(1)根據圓心在弦的中垂線上求得線段AC的垂直平分線方程為y=2x+3,可知圓心在這條線上,設圓心為M(a,2a+3)再有垂徑定理構造方程求解即可;(2)由直線和圓相切的性質得到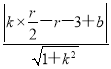 =r,圓心到直線的距離為半徑,再根據方程恒等得到
=r,圓心到直線的距離為半徑,再根據方程恒等得到
對應系數相等即可;
(1)由題意C(0,-2),A(-4,0),
所以線段AC的垂直平分線方程為y=2x+3.
設M(a,2a+3)(a>0),則圓M的方程為(x-a)2+(y-2a-3)2=r2.
圓心M到y軸的距離d=a,由r2=d2+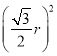 ,得a=
,得a=![]() .
.
所以圓M的方程為![]() +(y-r-3)2=r2.
+(y-r-3)2=r2.
(2)假設存在定直線l與動圓M均相切.當定直線的斜率不存在時,不合題意.
設直線l:y=kx+b,則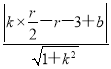 =r對任意r>0恒成立.
=r對任意r>0恒成立.
由![]() ,得
,得![]() r2+(k-2)(b-3)r+(b-3)2=(1+k2)r2.
r2+(k-2)(b-3)r+(b-3)2=(1+k2)r2.
所以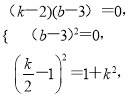 解得
解得![]() 或
或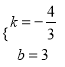
所以存在兩條直線y=3和4x+3y-9=0與動圓M均相切.


 超能學典應用題題卡系列答案
超能學典應用題題卡系列答案科目:高中數學 來源: 題型:
【題目】為了了解2013年某校高三學生的視力情況,隨機抽查了一部分學生視力,將調查結果分組,分組區間為![]() ,
,![]() ,… ,
,… ,![]() 經過數據處理,得到如右頻率分布表:
經過數據處理,得到如右頻率分布表:
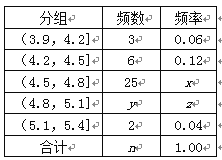
(1)求頻率分布表中未知量![]() 的值;
的值;
(2)從樣本中視力在![]() 和
和![]() 的所有同學中隨機抽取兩人,求兩人的視力差的絕對值低于0.5的概率.
的所有同學中隨機抽取兩人,求兩人的視力差的絕對值低于0.5的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某地區擬建立一個藝術博物館,采取競標的方式從多家建筑公司選取一家建筑公司,經過層層篩選,甲、乙兩家建筑公司進入最后的招標.現從建筑設計院聘請專家設計了一個招標方案:兩家公司從![]() 個招標問題中隨機抽取
個招標問題中隨機抽取![]() 個問題,已知這
個問題,已知這![]() 個招標問題中,甲公司可正確回答其中的
個招標問題中,甲公司可正確回答其中的![]() 道題目,而乙公司能正確回答毎道題目的概率均為
道題目,而乙公司能正確回答毎道題目的概率均為![]() ,甲、乙兩家公司對每題的回答都是相互獨立,互不影響的.
,甲、乙兩家公司對每題的回答都是相互獨立,互不影響的.
(1)求甲、乙兩家公司共答對![]() 道題目的概率;
道題目的概率;
(2)請從期望和方差的角度分析,甲、乙兩家哪家公司競標成功的可能性更大?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,直三棱柱![]() 中,各棱長均為6,
中,各棱長均為6, ![]() 分別是側棱
分別是側棱![]() 、
、![]() 上的點,且
上的點,且![]() .
.
(1)在![]() 上是否存在一點
上是否存在一點![]() ,使得
,使得![]() 平面
平面![]() ?證明你的結論;
?證明你的結論;
(2)求異面直線![]() 與
與![]() 所成角的余弦值.
所成角的余弦值.

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某書店銷售剛剛上市的某知名品牌的高三數學單元卷,按事先擬定的價格進行5天試銷,每種單價試銷1天,得到如表數據:
單價x(元) | 18 | 19 | 20 | 21 | 22 |
銷量y(冊) | 61 | 56 | 50 | 48 | 45 |
(1)求試銷5天的銷量的方差和y對x的回歸直線方程;
(2)預計今后的銷售中,銷量與單價服從(1)中的回歸方程,已知每冊單元卷的成本是14元,
為了獲得最大利潤,該單元卷的單價應定為多少元?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】2016年被業界稱為![]() (虛擬現實技術)元年,未來
(虛擬現實技術)元年,未來![]() 技術將給教育、醫療、娛樂、商業、交通旅游等多領域帶來極大改變,某
技術將給教育、醫療、娛樂、商業、交通旅游等多領域帶來極大改變,某![]() 教育設備生產企業有甲、乙兩類產品,其中生產一件甲產品需
教育設備生產企業有甲、乙兩類產品,其中生產一件甲產品需![]() 團隊投入15天時間,
團隊投入15天時間, ![]() 團隊投入20天時間,總費用10萬元,甲產品售價為15萬元/件;生產一件乙產品需
團隊投入20天時間,總費用10萬元,甲產品售價為15萬元/件;生產一件乙產品需![]() 團隊投入20天時間,
團隊投入20天時間, ![]() 團隊投入16天時間,總費用15萬元,乙產品售價為25萬元/件,
團隊投入16天時間,總費用15萬元,乙產品售價為25萬元/件, ![]() 、
、![]() 兩個團隊分別獨立運作.現某客戶欲以不超過200萬元訂購該企業甲、乙兩類產品,要求每類產品至少各3件,在期限180天內,為使企業總效益最佳,則最后交付的甲、乙兩類產品數之和為__________.
兩個團隊分別獨立運作.現某客戶欲以不超過200萬元訂購該企業甲、乙兩類產品,要求每類產品至少各3件,在期限180天內,為使企業總效益最佳,則最后交付的甲、乙兩類產品數之和為__________.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知圓![]() 經過點
經過點![]() ,
, ![]() ,并且直線
,并且直線![]() 平分圓
平分圓![]() .
.
(1)求圓![]() 的方程;
的方程;
(2)若直線![]() 與圓
與圓![]() 交于
交于![]() 兩點,是否存在直線
兩點,是否存在直線![]() ,使得
,使得![]() (
(![]() 為坐標原點),若存在,求出
為坐標原點),若存在,求出![]() 的值;若不存在,請說明理由.
的值;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】選修4-4:坐標系與參數方程
已知曲線![]() 的極坐標方程是
的極坐標方程是![]() ,以極點為原點,極軸為
,以極點為原點,極軸為![]() 軸的正半軸建立平面直角坐標系,直線
軸的正半軸建立平面直角坐標系,直線![]() 的參數方程為
的參數方程為 (
(![]() 為參數).
為參數).
(Ⅰ)寫出直線![]() 的普通方程與曲線
的普通方程與曲線![]() 的直角坐標方程;
的直角坐標方程;
(Ⅱ)設曲線![]() 經過伸縮變換
經過伸縮變換 得到曲線
得到曲線![]() ,若點
,若點![]() ,直線
,直線![]() 與
與![]() 交與
交與![]() ,
, ![]() ,求
,求![]() ,
, ![]() .
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com