Question

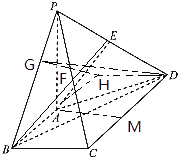
【題目】如圖，四棱錐P﹣ABCD的底面是直角梯形，∠ABC=∠BCD= ，AB=BC=1，CD=2，PA⊥平面ABCD，E是PD的中點．

（1）求證：AE∥平面PBC；
（2）若直線AE與直線BC所成角等于 ，求二面角D﹣PB﹣A平面角的余弦值．

Answer 1

【答案】
（1）證明：取PC中點F，連結EF、BF，

∴△PCD中，EF ，AB ，

∴EF AB，

∴四邊形ABFE為平行四邊形，

∵AE∥BF，AE平面PBC，BF平面PBC，

∴AE∥平面PBC．

（2）解：AE與直線BC所成角為 ， ，

∴BP= ，∴PA= ，

延長BA一倍到H，連結DH，再作HG⊥BP，連結DG，

則∠DGH是二面角D﹣PB﹣A的平面角，

DH=1，FG× ，HG= ，

∴tan∠DGH= ，

∴cos∠DGH= ．

∴二面角D﹣PB﹣A平面角的余弦值為 ．

【解析】（1）取PC中點F，連結EF、BF，推導出四邊形ABFE為平行四邊形，從而AE∥BF，由此能證明AE∥平面PBC．（2）AE與直線BC所成角為 ，延長BA一倍到H，連結DH，再作HG⊥BP，連結DG，∠DGH是二面角D﹣PB﹣A的平面角，由此能求出二面角D﹣PB﹣A平面角的余弦值．
【考點精析】根據題目的已知條件，利用直線與平面平行的判定的相關知識可以得到問題的答案，需要掌握平面外一條直線與此平面內的一條直線平行，則該直線與此平面平行；簡記為：線線平行，則線面平行．