
【題目】設函數f(x)= ![]() cos2x+sin2(x+
cos2x+sin2(x+ ![]() ). (Ⅰ)求f(x)的最小正周期和單調遞增區間;
). (Ⅰ)求f(x)的最小正周期和單調遞增區間;
(Ⅱ)當x∈[﹣ ![]() ,
, ![]() )時,求f(x)的取值范圍.
)時,求f(x)的取值范圍.
【答案】解:(Ⅰ)f(x)= ![]() cos2x+sin2(x+
cos2x+sin2(x+ ![]() ). f(x)=
). f(x)= ![]() cos2x+
cos2x+ ![]()
f(x)= ![]() cos2x+
cos2x+ ![]() sin2x+
sin2x+ ![]()
f(x)=sin(2x+ ![]() )+
)+ ![]() ,
,
最小正周期 ![]() ,
,
∵sinx單調遞增區間為[2kπ﹣ ![]() ,2kπ+
,2kπ+ ![]() ],(k∈Z)
],(k∈Z)
∴2x+ ![]() ∈[2kπ﹣
∈[2kπ﹣ ![]() ,2kπ+
,2kπ+ ![]() ],(k∈Z)
],(k∈Z)
解得:x∈[ ![]() ,
, ![]() ],(k∈Z)
],(k∈Z)
∴f(x)的最小正周期為π;單調遞增區間為[ ![]() ,
, ![]() ],(k∈Z)
],(k∈Z)
(Ⅱ)由(Ⅰ)得:f(x)=sin(2x+ ![]() )+
)+ ![]()
∵x∈[﹣ ![]() ,
, ![]() ),
),
∴2x+ ![]() ∈[
∈[ ![]() ,
, ![]() ],
],
由三角函數的圖像和性質:
可知:當2x+ ![]() =
= ![]() 時,f(x)取得最小值,即
時,f(x)取得最小值,即 ![]() =0.
=0.
當2x+ ![]() =
= ![]() 時,f(x)取得最大值,即
時,f(x)取得最大值,即 ![]() .
.
∴x∈[﹣ ![]() ,
, ![]() )時,f(x)的取值范圍在
)時,f(x)的取值范圍在 ![]()
【解析】(Ⅰ)先利用兩角和余差的基本公式將函數化為y=Asin(ωx+φ)的形式,再利用周期公式求函數的最小正周期,最后將內層函數看作整體,放到正弦函數的增區間上,解不等式得函數的單調遞增區間;(Ⅱ)x∈[﹣ ![]() ,
, ![]() )時,求出內層函數的取值范圍,結合三角函數的圖像和性質,求出f(x)的取值最大和最小值,即得到f(x)的取值范圍.
)時,求出內層函數的取值范圍,結合三角函數的圖像和性質,求出f(x)的取值最大和最小值,即得到f(x)的取值范圍.


科目:高中數學 來源: 題型:
【題目】正三棱錐P﹣ABC中,CM=2PM,CN=2NB,對于以下結論:
①二面角B﹣PA﹣C大小的取值范圍是( ![]() ,π);
,π);
②若MN⊥AM,則PC與平面PAB所成角的大小為 ![]() ;
;
③過點M與異面直線PA和BC都成 ![]() 的直線有3條;
的直線有3條;
④若二面角B﹣PA﹣C大小為 ![]() ,則過點N與平面PAC和平面PAB都成
,則過點N與平面PAC和平面PAB都成 ![]() 的直線有3條.
的直線有3條.
正確的序號是 . 
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,隔河看兩目標A、B,但不能到達,在岸邊選取相距 ![]() km的C、D兩點,并測得∠ACB=75°,∠BCD=45°,∠ADC=30°,∠ADB=45°(A、B、C、D在同一平面內),求兩目標A、B之間的距離.
km的C、D兩點,并測得∠ACB=75°,∠BCD=45°,∠ADC=30°,∠ADB=45°(A、B、C、D在同一平面內),求兩目標A、B之間的距離. 
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】選修4—4:坐標系與參數方程
點P是曲線C1:(x-2)2+y2=4上的動點,以坐標原點O為極點,x軸的正半軸為極軸
建立極坐標系,將點P繞極點O逆時針90得到點Q,設點Q的軌跡為曲線C2.
求曲線C1,C2的極坐標方程;
射線=![]() (>0)與曲線C1,C2分別交于A,B兩點,定點M(2,0),求MAB的面積
(>0)與曲線C1,C2分別交于A,B兩點,定點M(2,0),求MAB的面積
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】將函數y=sinx的圖象上所有點的橫坐標伸長到原來的2倍(縱坐標不變),再將所得的圖象向左平移 ![]() 個單位,得到的圖象對應的解析式是( )
個單位,得到的圖象對應的解析式是( )
A.y=sin(2x+ ![]() )
)
B.y=sin( ![]() x+
x+ ![]() )
)
C.y=sin( ![]() x+
x+ ![]() )
)
D.y=sin(2x+ ![]() )
)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為了增強市民的環境保護組織,某市面向全市征召n名義務宣傳志愿者,成立環境保護宣傳組織,現按年齡把該組織的成員分成5組:[20,25),[25,30),[30,35),[35,40),[40,45]. 得到的頻率分布直方圖如圖所示,已知該組織的成員年齡在[35,40)內有20人 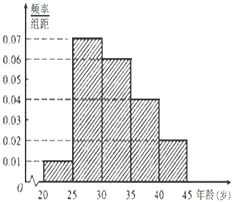
(1)求該組織的人數;
(2)若從該組織年齡在[20,25),[25,30),[30,35)內的成員中用分層抽樣的方法共抽取14名志愿者參加某社區的宣傳活動,問應各抽取多少名志愿者?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖, ![]() 為圓
為圓![]() 的直徑,點
的直徑,點![]() ,
, ![]() 在圓
在圓![]() 上,
上, ![]() ,矩形
,矩形![]() 和圓
和圓![]() 所在的平面互相垂直,已知
所在的平面互相垂直,已知![]() ,
, ![]() .
.
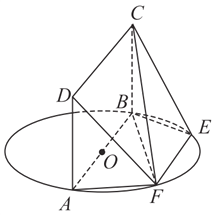
(Ⅰ)求證:平面![]() 平面
平面![]() ;
;
(Ⅱ)求直線![]() 與平面
與平面![]() 所成角的大小;
所成角的大小;
(Ⅲ)當![]() 的長為何值時,二面角
的長為何值時,二面角![]() 的大小為
的大小為![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,矩形ABCD中,AB=2BC=4,E為邊AB的中點,將△ADE沿直線DE翻轉成△A1DE.若M為線段A1C的中點,則在△ADE翻轉過程中: ①|BM|是定值;
②點M在圓上運動;
③一定存在某個位置,使DE⊥A1C;
④一定存在某個位置,使MB∥平面A1DE.
其中正確的命題是( )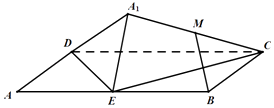
A.①②③
B.①②④
C.①③④
D.②③④
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數y=f(x+1)的定義域是[﹣1,3],則y=f(x2)的定義域是( )
A.[0,4]
B.[0,16]
C.[﹣2,2]
D.[1,4]
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com