
【題目】下列函數中,既是偶函數又在區間(﹣∞,0)上單調遞增的是( )
A.f(x)= ![]()
B.f(x)=x2+1
C.f(x)=x3
D.f(x)=2﹣x
【答案】A
【解析】解:選項A, ![]() ,∵f(﹣x)=
,∵f(﹣x)= ![]() =f(x),∴f(x)是偶函數,圖象關于y軸對稱. ∵f(x)=x﹣2 , ﹣2<0,∴f(x)在(0,+∞)單調遞減,
=f(x),∴f(x)是偶函數,圖象關于y軸對稱. ∵f(x)=x﹣2 , ﹣2<0,∴f(x)在(0,+∞)單調遞減,
∴根據對稱性知,f(x)在區間(﹣∞,0)上單調遞增; 適合題意.
選項B,f(x)=x2+1,是偶函數,在(0,+∞)上單調遞增,在區間(﹣∞,0)上單調遞減,不合題意.
選項C,f(x)=x3是奇函數,不是偶函數,不合題意.
選項D,f(x)=2﹣x在(﹣∞,+∞)單調遞減,不是奇函數,也不是偶函數,不合題意.
故選A.
【考點精析】本題主要考查了奇偶性與單調性的綜合的相關知識點,需要掌握奇函數在關于原點對稱的區間上有相同的單調性;偶函數在關于原點對稱的區間上有相反的單調性才能正確解答此題.


科目:高中數學 來源: 題型:
【題目】函數f(x)=sin2x+2 ![]() cos2x﹣
cos2x﹣ ![]() ,函數g(x)=mcos(2x﹣
,函數g(x)=mcos(2x﹣ ![]() )﹣2m+3(m>0),若存在x1 , x2∈[0,
)﹣2m+3(m>0),若存在x1 , x2∈[0, ![]() ],使得f(x1)=g(x2)成立,則實數m的取值范圍是( )
],使得f(x1)=g(x2)成立,則實數m的取值范圍是( )
A.(0,1]
B.[1,2]
C.[ ![]() ,2]
,2]
D.[ ![]() ,
, ![]() ]
]
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=sin(ωx+φ) ![]() 的最小正周期為π,
的最小正周期為π,
(1)求當f(x)為偶函數時φ的值;
(2)若f(x)的圖象過點( ![]() ,
, ![]() ),求f(x)的單調遞增區間.
),求f(x)的單調遞增區間.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某廠家舉行大型的促銷活動,經測算某產品當促銷費用為![]() 萬元時,銷售量
萬元時,銷售量![]() 萬件滿足
萬件滿足![]() (其中
(其中![]() ,
, ![]() 為正常數),現假定生產量與銷售量相等,已知生產該產品
為正常數),現假定生產量與銷售量相等,已知生產該產品![]() 萬件還需投入成本
萬件還需投入成本![]() 萬元(不含促銷費用),產品的銷售價格定為
萬元(不含促銷費用),產品的銷售價格定為![]() 萬元/萬件.
萬元/萬件.
(1)將該產品的利潤![]() 萬元表示為促銷費用
萬元表示為促銷費用![]() 萬元的函數;
萬元的函數;
(2)促銷費用投入多少萬元時,廠家的利潤最大.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在四棱錐P-ABCD中,PC⊥底面ABCD,底面ABCD是直角梯形,AB⊥AD,AB∥CD,AB=2AD=2CD=2,E是PB的中點.
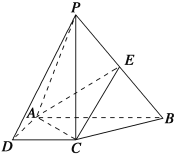
(1)求證:平面EAC⊥平面PBC;
(2)若二面角P-AC-E的余弦值為![]() ,求直線PA與平面EAC所成角的正弦值.
,求直線PA與平面EAC所成角的正弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】城市公交車的數量太多容易造成資源的浪費,太少又難以滿足乘客的需求,為此,某市公交公司在某站臺的60名候車的乘客中隨機抽取15人,將他們的候車時間作為樣本分成5組,如下表所示:
組別 | 一 | 二 | 三 | 四 | 五 |
候車時間(分鐘) |
|
|
|
|
|
人數 | 2 | 6 | 4 | 2 | 1 |
(1)估計這15名乘客的平均候車時間;
(2)估計這60 名乘客中候車時間少于10 分鐘的人數;
(3)若從上表第三、四組的6人中選2人作進一步的問卷調查,求抽到的2人恰好來自不同組的概率.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com