
【題目】已知函數![]() .
.
(1)若函數![]() 在
在![]() 處的切線斜率為2,試求a的值及此時的切線方程;
處的切線斜率為2,試求a的值及此時的切線方程;
(2)若函數![]() 在區間
在區間![]() (其中
(其中![]() …為自然對數的底數)上有唯一的零點,求實數a的取值范圍.
…為自然對數的底數)上有唯一的零點,求實數a的取值范圍.
【答案】(1)![]() ,
,![]() ;(2)
;(2)![]() 或
或![]() .
.
【解析】
(1)根據導數的幾何意義求解即可;
(2)討論參數![]() 的值,確定函數
的值,確定函數![]() 在區間
在區間![]() 的單調性,從而根據零點的個數,得出實數a的取值范圍.
的單調性,從而根據零點的個數,得出實數a的取值范圍.
(1)由![]() ,(
,(![]() ).
).
由已知![]() .
.
可得:![]()
又此時![]() .
.
所以所求的切線方程為:![]() .
.
即:![]()
(2)![]() ,其中
,其中![]()
①當![]() 時,
時,![]() 在區間
在區間![]() 恒成立,
恒成立,![]() 在區間
在區間![]() 單調遞增
單調遞增
又∵![]() ,∴函數
,∴函數![]() 在區間
在區間![]() 上有唯一的零點,符合題意.
上有唯一的零點,符合題意.
②當![]() 時,
時,![]() 在區間
在區間![]() 恒成立,
恒成立,![]() 在區間
在區間![]() 單調遞減
單調遞減
又∵![]() ,∴函數
,∴函數![]() 在區間
在區間![]() 上有唯一的零點,符合題意.
上有唯一的零點,符合題意.
③當![]() 時
時
(i)![]() 時,
時,![]() ,
,![]() 單調遞減
單調遞減
又∵![]() ,
,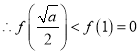 ,∴函數
,∴函數![]() 在區間
在區間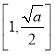 上有唯一的零點
上有唯一的零點
(ii)當![]() 時,
時,![]() ,
,![]() 單調遞增
單調遞增
∴要使![]() 在區間
在區間![]() 上有唯一的零點,只有當
上有唯一的零點,只有當![]() 時符合題意
時符合題意
即![]() ,即
,即![]()
∴![]() 時,函數
時,函數![]() 在區間
在區間![]() 上有唯一的零點;
上有唯一的零點;
∴綜上a的取值范圍是![]() 或
或![]() .
.


 陽光試卷單元測試卷系列答案
陽光試卷單元測試卷系列答案科目:高中數學 來源: 題型:
【題目】在全球抗擊新冠肺炎疫情期間,我國醫療物資生產企業加班加點生產口罩、防護服、消毒水等防疫物品,保障抗疫一線醫療物資供應,在國際社會上贏得一片贊譽.我國某口罩生產廠商在加大生產的同時.狠抓質量管理,不定時抽查口罩質量,該廠質檢人員從某日所生產的口罩中隨機抽取了100個,將其質量指標值分成以下五組:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,得到如下頻率分布直方圖.
,得到如下頻率分布直方圖.
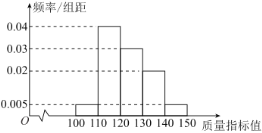
(1)規定:口罩的質量指標值越高,說明該口罩質量越好,其中質量指標值低于130的為二級口罩,質量指標值不低于130的為一級口罩.現從樣本口罩中利用分層抽樣的方法隨機抽取8個口罩,再從中抽取3個,記其中一級口罩個數為![]() ,求
,求![]() 的分布列及數學期望;
的分布列及數學期望;
(2)在2020年“五一”勞動節前,甲,乙兩人計劃同時在該型號口罩的某網絡購物平臺上分別參加![]() 、
、![]() 兩店各一個訂單“秒殺”搶購,其中每個訂單由
兩店各一個訂單“秒殺”搶購,其中每個訂單由![]() 個該型號口罩構成.假定甲、乙兩人在
個該型號口罩構成.假定甲、乙兩人在![]() 、
、![]() 兩店訂單“秒殺”成功的概率分別為
兩店訂單“秒殺”成功的概率分別為![]() ,
,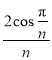 ,記甲、乙兩人搶購成功的訂單總數量、口罩總數量分別為
,記甲、乙兩人搶購成功的訂單總數量、口罩總數量分別為![]() ,
,![]() ,
,
①求![]() 的分布列及數學期望
的分布列及數學期望![]() ;
;
②求當![]() 的數學期望
的數學期望![]() 取最大值時正整數
取最大值時正整數![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】近幾年,電商行業的蓬勃發展帶動了快遞業的迅速增長,快遞公司攬收價格一般是采用“首重+續重”的計價方式.首重是指最低的計費重量,續重是指超過首重部分的計費重量,不滿一公斤按一公斤計費.某快遞網點將快件的攬收價格定為首重(不超過一公斤)8元,續重2元/公斤(例如,若一個快件的重量是0.6公斤,按8元計費;若一個快件的重量是1.4公斤,按![]() 元
元![]() 元
元![]() 元計費).根據歷史數據,得到該網點攬收快件重量的頻率分布直方圖如下圖所示
元計費).根據歷史數據,得到該網點攬收快件重量的頻率分布直方圖如下圖所示
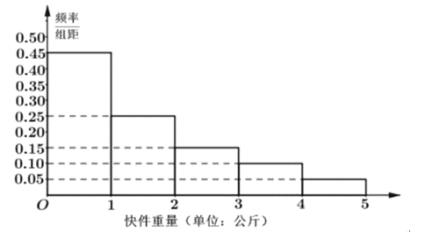
(1)根據樣本估計總體的思想,將頻率視作概率,求該網點攬收快件的平均價格;
(2)為了獲得更大的利潤,該網點對“一天中收發一件快遞的平均成本![]() (單位:元)與當天攬收的快遞件數
(單位:元)與當天攬收的快遞件數![]() (單位:百件)
(單位:百件)![]() 之間的關系”進行調查研究,得到相關數據如下表:
之間的關系”進行調查研究,得到相關數據如下表:
每天攬收快遞件數 | 2 | 3 | 4 | 5 | 8 |
每件快遞的平均成本 | 5.6 | 4.8 | 4.4 | 4.3 | 4.1 |
根據以上數據,技術人員分別根據甲、乙兩種不同的回歸模型,得到兩個回歸方程:
方程甲:![]() ,方程乙:
,方程乙:![]() .
.
①為了評價兩種模型的擬合效果,根據上表數據和相應回歸方程,將以下表格填寫完整(結果保留一位小數),分別計算模型甲與模型乙的殘差平方和![]() ,
,![]() ,并依此判斷哪個模型的擬合效果更好(備注:
,并依此判斷哪個模型的擬合效果更好(備注:![]() 稱為相應于點
稱為相應于點![]() 的殘差,殘差平方和
的殘差,殘差平方和![]() ;
;
每天攬收快遞件數 | 2 | 3 | 4 | 5 | 8 | |
每天快遞的平均成本 | 5.6 | 4.8 | 4.4 | 4.3 | 4.1 | |
模型甲 | 預報值 | 5.2 | 5.0 | 4.8 | ||
殘差 |
| 0.2 | 0.4 | |||
模型乙 | 預報值 | 5.5 | 4.8 | 4.5 | ||
預報值 |
| 0 | 0.1 | |||
②預計該網點今年6月25日(端午節)一天可以攬收1000件快遞,試根據①中確定的擬合效果較好的回歸模型估計該網點當天的總利潤(總利潤=(平均價格-平均成本)×總件數).
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知拋物線![]() ,與圓
,與圓![]() 有且只有兩個公共點.
有且只有兩個公共點.
(1)求拋物線![]() 的方程;
的方程;
(2)經過![]() 的動直線
的動直線![]() 與拋物線
與拋物線![]() 交于
交于![]() 兩點,試問在直線
兩點,試問在直線![]() 上是否存在定點
上是否存在定點![]() ,使得直線
,使得直線![]() 的斜率之和為直線
的斜率之和為直線![]() 斜率的
斜率的![]() 倍?若存在,求出定點
倍?若存在,求出定點![]() ;若不存在,請說明理由.
;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,四棱錐![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
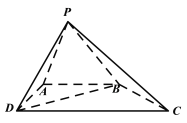
(1)求證:平面![]() 平面
平面![]() ;
;
(2)在線段![]() 上是否存在點
上是否存在點![]() ,使得平面
,使得平面![]() 與平面
與平面![]() 所成銳二面角為
所成銳二面角為![]() ?若存在,求
?若存在,求![]() 的值;若不存在,說明理由.
的值;若不存在,說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系![]() 中,動直線
中,動直線![]() 交拋物線
交拋物線![]() 于A,B兩點.
于A,B兩點.
(1)若![]() ,證明直線
,證明直線![]() 過定點,并求出該定點;
過定點,并求出該定點;
(2)點M為![]() 的中點,過點M作與y軸垂直的直線交拋物線
的中點,過點M作與y軸垂直的直線交拋物線![]() 于C點;點N為
于C點;點N為![]() 的中點,過點N作與y軸垂直的直線交拋物線
的中點,過點N作與y軸垂直的直線交拋物線![]() 于點P.設△
于點P.設△![]() 的面積
的面積![]() ,△
,△![]() 的面積為
的面積為![]() .
.
(i)若![]() 過定點
過定點![]() ,求使
,求使![]() 取最小值時,直線
取最小值時,直線![]() 的方程;
的方程;
(ii)求![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在四棱錐P-ABCD中,底面ABCD為正方形,PA⊥平面ABCD,PA=AB,E為線段PB的中點,F為線段BC上的動點.

(1)求證:AE⊥平面PBC;
(2)試確定點F的位置,使平面AEF與平面PCD所成的銳二面角為30°.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的離心率為
的離心率為![]() ,圓
,圓![]() 經過橢圓
經過橢圓![]() 的左,右焦點
的左,右焦點![]() .
.
(1)求橢圓![]() 的標準方程;
的標準方程;
(2)直線![]() 與橢圓
與橢圓![]() 交于點
交于點![]() ,線段
,線段![]() 的中點為
的中點為![]() ,
,![]() 的垂直平分線與
的垂直平分線與![]() 軸和
軸和![]() 軸分別交于
軸分別交于![]() 兩點,是否存在實數
兩點,是否存在實數![]() ,使得
,使得![]() 的面積與
的面積與![]() (
(![]() 為原點)的面積相等?若存在,求出
為原點)的面積相等?若存在,求出![]() 的值,若不存在,說明理由.
的值,若不存在,說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com