
【題目】十九大提出,堅決打贏脫貧攻堅戰,某幫扶單位為幫助定點扶貧村真脫貧,堅持扶貧同扶智相結合,幫助貧困村種植蜜柚,并利用電商進行銷售,為了更好地銷售,現從該村的蜜柚樹上隨機摘下了100個蜜柚進行測重,其質量分別在![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() (單位:克)中,其頻率分布直方圖如圖所示.
(單位:克)中,其頻率分布直方圖如圖所示.

(1)求質量落在![]() ,
, ![]() 兩組內的蜜柚的抽取個數,
兩組內的蜜柚的抽取個數,
(2)從質量落在![]() ,
, ![]() 內的蜜柚中隨機抽取2個,求這2個蜜柚質量均小于2000克的概率;
內的蜜柚中隨機抽取2個,求這2個蜜柚質量均小于2000克的概率;
 期末沖刺100分創新金卷完全試卷系列答案
期末沖刺100分創新金卷完全試卷系列答案科目:高中數學 來源: 題型:
【題目】橢圓![]() 的離心率為
的離心率為![]() ,且過點
,且過點![]() .
.
(1)求橢圓![]() 的方程;
的方程;
(2)設![]() 為橢圓
為橢圓![]() 上任一點,
上任一點, ![]() 為其右焦點,點
為其右焦點,點![]() 滿足
滿足![]() .
.
①證明: ![]() 為定值;
為定值;
②設直線![]() 與橢圓
與橢圓![]() 有兩個不同的交點
有兩個不同的交點![]() ,與
,與![]() 軸交于點
軸交于點![]() .若
.若![]() 成等差數列,求
成等差數列,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 兩焦點分別為
兩焦點分別為![]() 是橢圓在第一象限弧上一點,并滿足
是橢圓在第一象限弧上一點,并滿足![]() ,過P作傾斜角互補的兩條直線
,過P作傾斜角互補的兩條直線![]() 分別交橢圓于
分別交橢圓于![]() 兩點.
兩點.
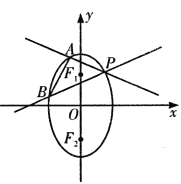
(1)求![]() 點坐標;
點坐標;
(2)求證:直線![]() 的斜率為定值;
的斜率為定值;
(3)求![]() 面積的最大值.
面積的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知集合A={y|y= ![]() },B={x|y=lg(x﹣2x2)},則R(A∩B)=( )
},B={x|y=lg(x﹣2x2)},則R(A∩B)=( )
A.[0, ![]() )
)
B.(﹣∞,0)∪[ ![]() ,+∞)
,+∞)
C.(0, ![]() )
)
D.(﹣∞,0]∪[ ![]() ,+∞)
,+∞)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系中,拋物線C的頂點在原點O,過點![]() ,其焦點F在x軸上.
,其焦點F在x軸上.
![]() 求拋物線C的標準方程;
求拋物線C的標準方程;
![]() 斜率為1且與點F的距離為
斜率為1且與點F的距離為![]() 的直線
的直線![]() 與x軸交于點M,且點M的橫坐標大于1,求點M的坐標;
與x軸交于點M,且點M的橫坐標大于1,求點M的坐標;
![]() 是否存在過點M的直線l,使l與C交于P、Q兩點,且
是否存在過點M的直線l,使l與C交于P、Q兩點,且![]() 若存在,求出直線l的方程;若不存在,說明理由.
若存在,求出直線l的方程;若不存在,說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】定義下凸函數如下:設f(x)為區間I上的函數,若對任意的x1 , x2∈I總有f( ![]() )≥
)≥ ![]() ,則稱f(x)為I上的下凸函數,某同學查閱資料后發現了下凸函數有如下判定定理和性質定理: 判定定理:f(x)為下凸函數的充要條件是f″(x)≥0,x∈I,其中f″(x)為f(x)的導函數f′(x)的導數.
,則稱f(x)為I上的下凸函數,某同學查閱資料后發現了下凸函數有如下判定定理和性質定理: 判定定理:f(x)為下凸函數的充要條件是f″(x)≥0,x∈I,其中f″(x)為f(x)的導函數f′(x)的導數.
性質定理:若函數f(x)為區間I上的下凸函數,則對I內任意的x1 , x2 , …,xn , 都有 ![]() ≥f(
≥f( ![]() ).
).
請問:在△ABC中,sinA+sinB+sinC的最大值為 .
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=xlnx.
(Ⅰ)設函數g(x)= ![]() ,求g(x)的單調區間;
,求g(x)的單調區間;
(Ⅱ)若方程f(x)=t有兩個不相等的實數根x1 , x2 , 求證:x1+x2 ![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在直角坐標系中,以原點O為極點,x軸為正半軸為極軸,建立極坐標系.設曲線C: ![]() (α為參數);直線l:ρ(cosθ+sinθ)=4.
(α為參數);直線l:ρ(cosθ+sinθ)=4.
(Ⅰ)寫出曲線C的普通方程和直線l的直角坐標方程;
(Ⅱ)求曲線C上的點到直線l的最大距離.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=|x+1|﹣|x﹣2|.
(Ⅰ)求不等式f(x)≥1的解集;
(Ⅱ)若不等式f(x)≥x2﹣x+m的解集非空,求m的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com