【題目】下列說法正確的是( )
A.若“
”為真命題，則“
”為真命題
B.命題“
”的否定是“
”
C.命題“若
，則
”的逆否命題為真命題
D.“
”是“
”的必要不充分條件
名校課堂系列答案科目：高中數學 來源： 題型：
【題目】在直角坐標坐標系
中，曲線
的參數方程為
（
為參數），曲線
： 
.以
為極點， 
軸的非負半軸為極軸，與直角坐標系
取相同的長度單位，建立極坐標系.
（1）求曲線
的極坐標方程；
（2）射線
（
）與曲線
的異于極點的交點為
，與曲線
的交點為
，求
.
【答案】(1) 
的極坐標方程為
， 
的極坐標方程為
；(2) 
.
【解析】試題分析：（1）先根據三角函數平方關系消參數得曲線
，再根據
將曲線
的
極坐標方程；（2）將
代人曲線
的極坐標方程，再根據
求
.
試題解析：（1）曲線
的參數方程
（
為參數）
可化為普通方程
，
由
，可得曲線
的極坐標方程為
，
曲線
的極坐標方程為
.
（2）射線
（
）與曲線
的交點
的極徑為
，
射線
（
）與曲線
的交點
的極徑滿足
，解得
，
所以
.
【題型】解答題
【結束】
23
【題目】設函數
．
（1）設
的解集為
，求集合；
（2）已知
為（1）中集合中的最大整數，且
（其中
，
，
為正實數），求證：
．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，設拋物線C1:
的準線1與x軸交于橢圓C2：
的右焦點F2，F1為C2的左焦點.橢圓的離心率為
，拋物線C1與橢圓C2交于x軸上方一點P，連接PF1并延長其交C1于點Q，M為C1上一動點，且在P，Q之間移動.
（1）當
取最小值時，求C1和C2的方程；
（2）若△PF1F2的邊長恰好是三個連續的自然數，當△MPQ面積取最大值時，求面積最大值以及此時直線MP的方程.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】在直角坐標系
中，曲線
的參數方程為
為參數且
，
，
，曲線
的參數方程為
為參數），以
為極點，
軸正半軸為極軸建立極坐標系，曲線
的極坐標方程為
．
（1）求的普通方程及的直角坐標方程；
（2）若曲線與曲線
分別交于點
，
，求
的最大值．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】為豐富學生課外生活，某市組織了高中生鋼筆書法比賽，比賽分兩個階段進行：第一階段由評委給出所有參賽作品評分，并確定優勝者；第二階段為附加賽，參賽人員由組委會按規則另行確定.數據統計員對第一階段的分數進行了統計分析，這些分數
都在
內，在以組距為5畫分數的頻率分布直方圖（設“
”)時，發現
滿足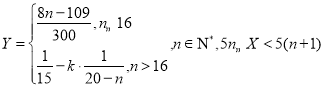
.
（1）試確定
的所有取值，并求
；
（2）組委會確定：在第一階段比賽中低于85分的參賽者無緣獲獎也不能參加附加賽；分數在
的參賽者評為一等獎；分數在
的同學評為二等獎，但通過附加賽有
的概率提升為一等獎；分數在
的同學評為三等獎，但通過附加賽有
的概率提升為二等獎（所有參加附加賽的獲獎人員均不降低獲獎等級）.已知學生
和
均參加了本次比賽，且學生在第一階段評為二等獎.
（
）求學生最終獲獎等級不低于學生的最終獲獎等級的概率；
（
）已知學生和都獲獎，記
兩位同學最終獲得一等獎的人數為
，求的分布列和數學期望.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】在中國決勝全面建成小康社會的關鍵之年，如何更好地保障和改善民生，如何切實增強政策“獲得感”，成為2019年全國兩會的重要關切．某地區為改善民生調研了甲、乙、丙、丁、戊5個民生項目，得到如下信息：
①若該地區引進甲項目，就必須引進與之配套的乙項目；
②丁、戊兩個項目與民生密切相關，這兩個項目至少要引進一個；
③乙、丙兩個項目之間有沖突，兩個項目只能引進一個；
④丙、丁兩個項目關聯度較高，要么同時引進，要么都不引進；
⑤若引進項目戊，甲、丁兩個項目也必須引進．
則該地區應引進的項目為______．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，三棱柱ABC-A1B1C1中，側面BCC1B1是菱形，AC=BC=2，∠CBB1=
，點A在平面BCC1B1上的投影為棱BB1的中點E．
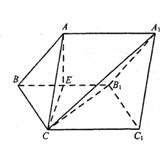
（1）求證：四邊形ACC1A1為矩形；
（2）求二面角E-B1C-A1的平面角的余弦值．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某省級示范高中高三年級對各科考試的評價指標中，有“難度系數“和“區分度“兩個指標中，難度系數
，區分度
.
（1）某次數學考試(滿分為150分)，隨機從實驗班和普通班各抽取三人，實驗班三人的成績分別為147，142，137；普通班三人的成績分別為97，102，113.通過樣本估計本次考試的區分度(精確0.01).
（2）如表表格是該校高三年級6次數學考試的統計數據：
難度系數x | 0.64 | 0.71 | 0.74 | 0.76 | 0.77 | 0.82 |
區分度y | 0.18 | 0.23 | 0.24 | 0.24 | 0.22 | 0.15 |
①計算相關系數r，|r|<0.75時，認為相關性弱；|r|≥0.75時，認為相關性強.通過計算說明，能否利用線性回歸模型描述y與x的關系(精確到0.01).
②ti=|xi﹣0.74|(i=1，2，…，6)，求出y關于t的線性回歸方程，并預測x=0.75時y的值(精確到0.01).
附注：參考數據：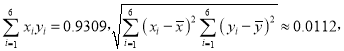
參考公式：相關系數
r，回歸直線
的斜率和截距的最小二乘估計分別為
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
