
(13分) (理科)已知雙曲線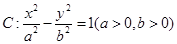 與橢圓
與橢圓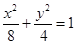 有公共焦點,且以拋物線
有公共焦點,且以拋物線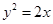 的準線為雙曲線
的準線為雙曲線 的一條準線.動直線
的一條準線.動直線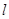 過雙曲線
過雙曲線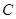 的右焦點
的右焦點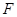 且與雙曲線的右支交于
且與雙曲線的右支交于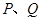 兩點.
兩點.
(1)求雙曲線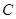 的方程;
的方程;
(2)無論直線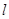 繞點
繞點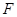 怎樣轉動,在雙曲線
怎樣轉動,在雙曲線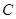 上是否總存在定點
上是否總存在定點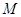 ,使
,使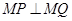 恒成立?若存在,求出點
恒成立?若存在,求出點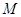 的坐標,若不存在,請說明理由.
的坐標,若不存在,請說明理由.
(1)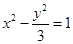
(2)雙曲線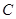 上存在定點
上存在定點 ,使
,使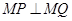 恒成立
恒成立
【解析】(理科)解:(1)設 ,則由題意有:
,則由題意有:
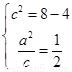 ∴
∴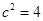 ,
,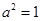 ,
,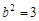
故雙曲線 的方程為
的方程為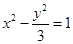 ,
…………… 4分
,
…………… 4分
(2)解法一:由(1)得點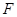 為
為
當直線l的斜率存在時,設直線方程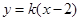 ,
,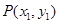 ,
,
將方程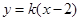 與雙曲線方程聯立消去
與雙曲線方程聯立消去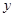 得:
得: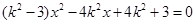 ,
,
∴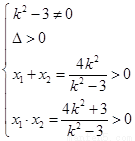 解得
解得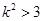 …………… 6分
…………… 6分
假設雙曲線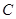 上存在定點
上存在定點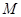 ,使
,使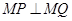 恒成立,設為
恒成立,設為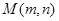
則: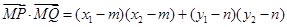
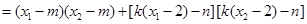
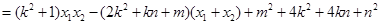
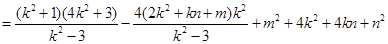
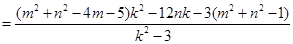
∵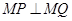 ,∴
,∴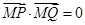 ,
,
故得: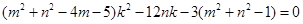 對任意的
對任意的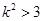 恒成立,
恒成立,
∴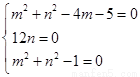 ,解得
,解得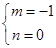
∴當點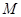 為
為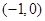 時,
時,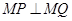 恒成立;
…………… 10分
恒成立;
…………… 10分
當直線l的斜率不存在時,由 ,
,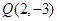 知點
知點 使得
使得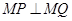 也成立.
也成立.
又因為點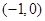 是雙曲線
是雙曲線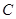 的左頂點,
…………… 12分
的左頂點,
…………… 12分
所以雙曲線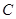 上存在定點
上存在定點 ,使
,使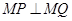 恒成立. ……………
13分
恒成立. ……………
13分
解法二(略解):當直線l的斜率不存在時,由 ,
,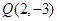 ,
,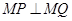 ,且點
,且點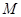 在雙曲線
在雙曲線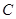 上可求得
上可求得 ,
,
當直線l的斜率存在時,將 ,
,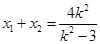 ,
,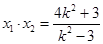 代入
代入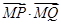 ,經計算發現
,經計算發現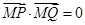 對任意的
對任意的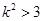 恒成立,從而恒有
恒成立,從而恒有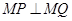 成立.
成立.
因而雙曲線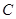 上存在定點
上存在定點 ,使
,使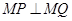 恒成立.
恒成立.


科目:高中數學 來源:2014屆安徽省高一元月文理分班考試數學 題型:解答題
(13分,理科做)已知函數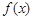 的定義域為
的定義域為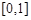 ,且同時滿足:①
,且同時滿足:①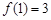 ;②
;②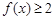 恒成立;③若
恒成立;③若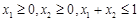 ,則有
,則有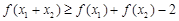 .
.
(1)試求函數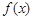 的最大值和最小值;
的最大值和最小值;
(2)試比較 與
與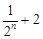 的大小
的大小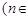 N);
N);
(3)某人發現:當x= (nÎN)時,有f(x)<2x+2.由此他提出猜想:對一切xÎ(0,1
(nÎN)時,有f(x)<2x+2.由此他提出猜想:對一切xÎ(0,1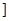 ,都有
,都有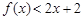 ,請你判斷此猜想是否正確,并說明理由.
,請你判斷此猜想是否正確,并說明理由.
查看答案和解析>>
科目:高中數學 來源:2010年重慶市高二下學期期中考試數學(文) 題型:解答題
16. (本小題滿分13分) 從4名文科教師和3名理科教師中任選3人擔任班主任.(寫出過程,最后結果用分數表示)
(1) 求所選3人都是理科教師的概率;
(2) 求所選3人中恰有1名理科教師的概率;
(3) 求所選3人中至少有1名理科教師的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
(本小題滿分13分)
已知正方體ABCD-A'B'C'D'的棱長為1,點M是棱AA'的中點,點O是對角線BD'的中點.
(Ⅰ)求證:OM為異面直線AA'和BD'的公垂線;
 (Ⅱ)求二面角M-BC'-B'的大小;
(Ⅱ)求二面角M-BC'-B'的大小;
(Ⅲ)求三棱錐M-OBC的體積(理科做,文科不做)
查看答案和解析>>
科目:高中數學 來源:2011-2012學年廣東省高三第五次階段考試理科數學試卷(解析版) 題型:解答題
某校從參加高三年級理科綜合物理考試的學生中隨機抽出 名學生,將其數學成績(均為整數)分成六段
名學生,將其數學成績(均為整數)分成六段 ,
, …
… 后得到如下部分頻率分布直方圖.觀察圖形的信息,回答下列問題:
后得到如下部分頻率分布直方圖.觀察圖形的信息,回答下列問題:
(Ⅰ)求分數在 內的頻率,并補全這個頻率分布直方圖;
內的頻率,并補全這個頻率分布直方圖;
(Ⅱ)統計方法中,同一組數據常用該組區間的中點值作為代表,據此估計本次考試的
平均分;
(Ⅲ)若從 名學生中隨機抽取
名學生中隨機抽取 人,抽到的學生成績在
人,抽到的學生成績在 記
記 分,在
分,在 記
記 分,
分,
在 記
記 分,用
分,用 表示抽取結束后的總記分,求
表示抽取結束后的總記分,求 的分布列和數學期望.
的分布列和數學期望.

【解析】(1)中利用直方圖中面積和為1,可以求解得到分數在 內的頻率為
內的頻率為
(2)中結合平均值可以得到平均分為:
(3)中用 表示抽取結束后的總記分x, 學生成績在
表示抽取結束后的總記分x, 學生成績在 的有
的有 人,在
人,在 的有
的有 人,在
人,在 的有
的有 人,結合古典概型的概率公式求解得到。
人,結合古典概型的概率公式求解得到。
(Ⅰ)設分數在 內的頻率為
內的頻率為 ,根據頻率分布直方圖,則有
,根據頻率分布直方圖,則有 ,可得
,可得 ,所以頻率分布直方圖如右圖.……4分
,所以頻率分布直方圖如右圖.……4分


(求解頻率3分,畫圖1分)
(Ⅱ)平均分為: ……7分
……7分
(Ⅲ)學生成績在 的有
的有 人,在
人,在 的有
的有 人,
人,
在 的有
的有 人.并且
人.并且 的可能取值是
的可能取值是 . ………8分
. ………8分
則 ;
; ;
;
 ;
;
 ;
; .(每個1分)
.(每個1分)
所以 的分布列為
的分布列為
|
|
0 |
1 |
2 |
3 |
4 |
|
|
|
|
|
|
|
…………………13分

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com