
| 1 |
| an |
| n |
| an |
| 1 |
| an |
| n |
| an |
| 1 |
| an+1 |
| 2 |
| an |
| 1 |
| an+1 |
| 1 |
| an |
| 1 |
| a1 |
| 1 |
| an |
| 1 |
| an |
| 1 |
| an |
| 1 |
| an |
| n |
| an |
| n |
| an |
| n(n+1) |
| 2 |


 活力試卷系列答案
活力試卷系列答案 課課優(yōu)能力培優(yōu)100分系列答案
課課優(yōu)能力培優(yōu)100分系列答案
| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
| 1 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
| A、A>B>C |
| B、A>C>B |
| C、B>A>C |
| D、C>B>A |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
| x2 |
| a2 |
| y2 |
| b2 |
| 3 |
| 2 |
| 1 |
| 2 |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
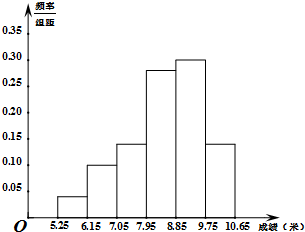 某市為了了解今年高中畢業(yè)生的體能情況,從本市某高中畢業(yè)班中抽取了一個班進(jìn)行鉛球測試,成績在8.0米(精確到0.1米)以上的為合格,把所得數(shù)據(jù)進(jìn)行整理后,分成六組畫出頻率分布直方圖的一部分,如圖,已知從左到右前5個小組的頻率分別為0.04,0.10,0.14,0.28,0.30,第六小組的頻數(shù)是7.
某市為了了解今年高中畢業(yè)生的體能情況,從本市某高中畢業(yè)班中抽取了一個班進(jìn)行鉛球測試,成績在8.0米(精確到0.1米)以上的為合格,把所得數(shù)據(jù)進(jìn)行整理后,分成六組畫出頻率分布直方圖的一部分,如圖,已知從左到右前5個小組的頻率分別為0.04,0.10,0.14,0.28,0.30,第六小組的頻數(shù)是7.查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
| 暈機(jī) | 不會暈機(jī) | 合計 | |
| 男學(xué)生 | 28 | 56 | |
| 女學(xué)生 | 56 | ||
| 合計 | 140 |
| n(ad-bc)2 |
| (a+b)(c+d)(a+c)(b+d) |
| P(K2≥k) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
 如圖,ABCD是邊長為2的正方形,ED⊥平面ABCD,ED=1,EF∥BD且EF=
如圖,ABCD是邊長為2的正方形,ED⊥平面ABCD,ED=1,EF∥BD且EF=| 1 |
| 2 |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
| x2 |
| a2 |
| y2 |
| b2 |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
| x2 | ||||
|
| y2 | ||||
|
| π |
| 4 |
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com