【題目】如圖，在平面直角坐標系xOy中，已知橢圓
(a＞b＞0)的離心率為
，長軸長為4.過橢圓的左頂點A作直線l，分別交橢圓和圓x2＋y2＝a2于相異兩點P，Q.
(1)若直線l的斜率為
，求
的值；
(2)若
，求實數(shù)λ的取值范圍.
【答案】（1）
（2）0＜λ＜1.
【解析】試題分析：
首先求得橢圓方程為
，圓的方程為
.
(1)法一：直線方程為
，與橢圓方程聯(lián)立可得
，則
，結(jié)合圓的性質(zhì)可得
,則
.
法二：聯(lián)立直線方程與橢圓方程可得： 
，則
.
(2)由題意可得
，設(shè)直線l：y＝k(x＋2)，與橢圓方程聯(lián)立可得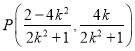
，據(jù)此可得： 
，同理可得
，則
.
試題解析：
由題意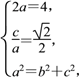得
解得
所以橢圓的方程為
＋
＝1，圓的方程為x2＋y2＝4.
(1)法一 直線l的方程為y＝
(x＋2)，
由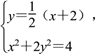
得3x3＋4x－4＝0.
解得xA＝－2，xP＝
，所以P
.
所以AP＝
＝
.
又因為原點O到直線l的距離d＝
＝
，
所以AQ＝2
＝
，所以
＝
＝
.
法二 由
得3y2－4y＝0，所以yP＝
.
由
得5y2－8y＝0，所以yQ＝
.
所以＝
＝×
＝.
(2)若
＝λ
，則λ＝
－1，
設(shè)直線l：y＝k(x＋2)，
由
得(2k2＋1)x2＋8k2x＋8k2－4＝0，
即(x＋2)[(2k2＋1)x＋(4k2－2)]＝0，
所以xA＝－2，xP＝
，得P
.
所以AP2＝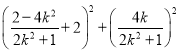
＝
，
即AP＝
.同理可得AQ＝
.
所以λ＝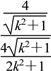
－1＝1－
.
由題意知k2＞0，所以0＜λ＜1.
科目：高中數(shù)學 來源： 題型：
【題目】如圖，
是
的直徑，PA垂直于所在的平面，C是圓周上不同于A，B的一動點.
（1）證明：
是直角三角形；
（2）若
，且當直線
與平面
所成角的正切值為
時，求直線與平面
所成角的正弦值.
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】某賽季，甲、乙兩名籃球運動員都參加了
場比賽，他們所有比賽得分的情況如下：
甲：
；
乙：
.
(1)求甲、乙兩名運動員得分的中位數(shù)．
(2)分別求甲、乙兩名運動員得分的平均數(shù)、方差，你認為哪位運動員的成績更穩(wěn)定？
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】某大學進行自主招生時,需要進行邏輯思維和閱讀表達兩項能力的測試.學校對參加測試的200名學生的邏輯思維成績、閱讀表達成績以及這兩項的總成績進行了排名.其中甲、乙、丙三位同學的排名情況如下圖所示:
得出下面四個結(jié)論:
①甲同學的邏輯排名比乙同學的邏輯排名更靠前
②乙同學的邏輯思維成績排名比他的閱讀表達成績排名更靠前
③甲、乙、丙三位同學的邏輯思維成績排名中,甲同學更靠前
④甲同學的閱讀表達成績排名比他的邏輯思維成績排名更靠前
則所有正確結(jié)論的序號是_________.
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】已知函數(shù)
.
（Ⅰ）當
時,（i）求曲線
在點
處的切線方程;
（ii）求函數(shù)
的單調(diào)區(qū)間；
（Ⅱ）若
,求證: 
.
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】在平面直角坐標系xOy中，中心在原點的橢圓C的上焦點為
，離心率等于
．
求橢圓C的方程；
設(shè)過且不垂直于坐標軸的動直線l交橢圓C于A、B兩點，問：線段OF上是否存在一點D，使得以DA、DB為鄰邊的平行四邊形為菱形？作出判斷并證明．
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】設(shè)甲、乙兩位同學上學期間，每天
之前到校的概率均為
.假定甲、乙兩位同學到校情況互不影響，且任一同學每天到校情況相互獨立.
（1）設(shè)甲同學上學期間的三天中之前到校的天數(shù)為
，求
，
，
，
時的概率
，
，
，
；
（2）設(shè)
為事件“上學期間的三天中，甲同學在之前到校的天數(shù)比乙同學在之前到校的天數(shù)恰好多
”，求事件發(fā)生的概率.
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】已知向量
（1）若
分別表示將一枚質(zhì)地均勻的正方體骰子(六個面的點數(shù)分別為1,2,3,4,5,6)先后拋擲兩次時第一次，第二次出現(xiàn)的點數(shù)，求滿足
的概率；
（2）若在連續(xù)區(qū)間[1,6]上取值，求滿足
的概率．
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
