
【題目】如圖四棱錐![]() 中,
中,![]() 底面
底面![]() ,
,![]() 是邊長為2的等邊三角形,且
是邊長為2的等邊三角形,且![]() ,
,![]() ,點
,點![]() 是棱
是棱![]() 上的動點.
上的動點.
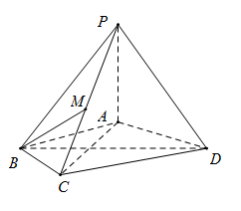
(I)求證:平面![]() 平面
平面![]() ;
;
(Ⅱ)當線段![]() 最小時,求直線
最小時,求直線![]() 與平面
與平面![]() 所成角的正弦值.
所成角的正弦值.
【答案】(I)證明見解析;(Ⅱ)![]() .
.
【解析】
(Ⅰ)由![]() 底面
底面![]() 可得
可得![]() .取
.取![]() 的中點
的中點![]() ,連接
,連接![]() ,根據等腰三角形的性質可得
,根據等腰三角形的性質可得![]() ,于是得到
,于是得到![]() 平面
平面![]() ,根據面面垂直的判定可得所證結論.(Ⅱ)取
,根據面面垂直的判定可得所證結論.(Ⅱ)取![]() 中點
中點![]() ,連接
,連接![]() ,可證得
,可證得![]() ,建立空間直角坐標系.然后根據向量的共線得到點
,建立空間直角坐標系.然后根據向量的共線得到點![]() 的坐標,再根據線段
的坐標,再根據線段![]() 最短得到點
最短得到點![]() 的位置,進而得到
的位置,進而得到![]() .求出平面
.求出平面![]() 的法向量后根據線面角與向量夾角間的關系可得所求.
的法向量后根據線面角與向量夾角間的關系可得所求.
(Ⅰ)證明:∵![]() 底面
底面![]() ,
,![]() 底面
底面![]() ,
,
∴![]() .
.
取![]() 的中點
的中點![]() ,連接
,連接![]() ,
,
∵![]() 是等邊三角形,
是等邊三角形,![]() ,
,
∴![]() ,
,![]() ,
,
∴點![]() 共線,從而得
共線,從而得![]() ,
,
又![]() ,
,
∴![]() 平面
平面![]() ,
,
∵![]() 平面
平面![]() ,
,
∴平面![]() 平面
平面![]() .
.
(Ⅱ)解:取![]() 中點
中點![]() ,連接
,連接![]() ,則
,則![]() ,
,
∴![]() 底面
底面![]() ,
,
∴![]() 兩兩垂直.
兩兩垂直.
以![]() 為原點如圖建立空間直角坐標系
為原點如圖建立空間直角坐標系![]() ,
,
則![]() ,
,
∴![]() ,
,
設平面![]() 的法向量為
的法向量為![]() ,
,
由 ,得
,得![]() ,
,
令![]() ,得
,得![]() .
.
設![]() ,則
,則![]() ,
,
∴![]() ,
,
∴當![]() 時,
時,![]() 有最小值,且
有最小值,且![]() ,此時
,此時![]() .
.
設直線![]() 與平面
與平面![]() 所成角為
所成角為![]() ,
,
則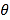 ,
,
∴直線![]() 與平面
與平面![]() 所成角的正弦值為
所成角的正弦值為![]() .
.


科目:高中數學 來源: 題型:
【題目】某科研團隊研發了一款快速檢測某種疾病的試劑盒.為了解該試劑盒檢測的準確性,質檢部門從某地區(人數眾多)隨機選取了![]() 位患者和
位患者和![]() 位非患者,用該試劑盒分別對他們進行檢測,結果如下:
位非患者,用該試劑盒分別對他們進行檢測,結果如下:
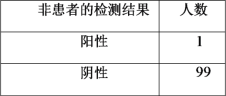
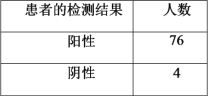
(1)從該地區患者中隨機選取一人,對其檢測一次,估計此患者檢測結果為陽性的概率;
(2)從該地區患者中隨機選取![]() 人,各檢測一次,假設每位患者的檢測結果相互獨立,以
人,各檢測一次,假設每位患者的檢測結果相互獨立,以![]() 表示檢測結果為陽性的患者人數,利用(1)中所得概率,求
表示檢測結果為陽性的患者人數,利用(1)中所得概率,求![]() 的分布列和數學期望;
的分布列和數學期望;
(3)假設該地區有![]() 萬人,患病率為
萬人,患病率為![]() .從該地區隨機選取一人,用該試劑盒對其檢測一次.若檢測結果為陽性,能否判斷此人患該疾病的概率超過
.從該地區隨機選取一人,用該試劑盒對其檢測一次.若檢測結果為陽性,能否判斷此人患該疾病的概率超過![]() ?并說明理由.
?并說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系xOy中,直角三角形ABC的三個頂點都在橢圓![]() 上,其中A(0,1)為直角頂點.若該三角形的面積的最大值為
上,其中A(0,1)為直角頂點.若該三角形的面積的最大值為![]() ,則實數a的值為_____.
,則實數a的值為_____.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】阿基米德是古希臘偉大的哲學家、數學家、物理學家,對幾何學、力學等學科作出過卓越貢獻.為調查中學生對這一偉大科學家的了解程度,某調查小組隨機抽取了某市的100名高中生,請他們列舉阿基米德的成就,把能列舉阿基米德成就不少于3項的稱為“比較了解”,少于三項的稱為“不太了解”.他們的調查結果如下:
0項 | 1項 | 2項 | 3項 | 4項 | 5項 | 5項以上 | |
理科生(人) | 1 | 10 | 17 | 14 | 14 | 10 | 4 |
文科生(人) | 0 | 8 | 10 | 6 | 3 | 2 | 1 |
(1)完成如下![]() 列聯表,并判斷是否有
列聯表,并判斷是否有![]() 的把握認為,了解阿基米德與選擇文理科有關?
的把握認為,了解阿基米德與選擇文理科有關?
比較了解 | 不太了解 | 合計 | |
理科生 | |||
文科生 | |||
合計 |
(2)在抽取的100名高中生中,按照文理科采用分層抽樣的方法抽取10人的樣本.
(i)求抽取的文科生和理科生的人數;
(ii)從10人的樣本中隨機抽取3人,用![]() 表示這3人中文科生的人數,求
表示這3人中文科生的人數,求![]() 的分布列和數學期望.
的分布列和數學期望.
參考數據:
| 0.100 | 0.050 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |
![]() ,
,![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在△ABC中,a![]() ,c
,c![]() ,________.(補充條件)
,________.(補充條件)
(1)求△ABC的面積;
(2)求sin(A+B).
從①b=4,②cosB![]() ,③sinA
,③sinA![]() 這三個條件中任選一個,補充在上面問題中并作答.
這三個條件中任選一個,補充在上面問題中并作答.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某貧困地區共有1500戶居民,其中平原地區1050戶,山區450戶.為調查該地區2017年家庭收入情況,從而更好地實施“精準扶貧”,采用分層抽樣的方法,收集了150戶家庭2017年年收入的樣本數據(單位:萬元).

(1)應收集多少戶山區家庭的樣本數據?
(2)根據這150個樣本數據,得到2017年家庭收入的頻率分布直方圖(如圖所示),其中樣本數據分組區間為(0,0.5],(0.5,1],(1,1.5],(1.5,2],(2,2.5],(2.5,3].如果將頻率視為概率,估計該地區2017年家庭收入超過1.5萬元的概率;
(3)樣本數據中,有5戶山區家庭的年收入超過2萬元,請完成2017年家庭收入與地區的列聯表,并判斷是否有90%的把握認為“該地區2017年家庭年收入與地區有關”?
超過2萬元 | 不超過2萬元 | 總計 | |
平原地區 | |||
山區 | 5 | ||
總計 |
附:
P(K2≥k0) | 0.100 | 0.050 | 0.010 | 0.001 |
k0 | 2.706 | 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】2020年1月22日,國新辦發布消息:新型冠狀病毒來源于武漢一家海鮮市場非法銷售的野生動.專家通過全基因組比對發現此病毒與2003年的非典冠狀病毒以及此后的中東呼吸綜合征冠狀病毒,分別達到70%和40%的序列相似性.這種新型冠狀病毒對人們的健康生命帶來了嚴重威脅因此,某生物疫苗研究所加緊對新型冠狀病毒疫苗進行實驗,并將某一型號疫苗用在動物小白鼠身上進行科研和臨床實驗,得到統計數據如下:
未感染病毒 | 感染病毒 | 總計 | |
未注射疫苗 | 20 |
|
|
注射疫苗 | 30 |
|
|
總計 | 50 | 50 | 100 |
現從所有試驗小白鼠中任取一只,取到“注射疫苗”小白鼠的概率為![]() .
.
(1)求![]() 列聯表中的數據
列聯表中的數據![]() ,
,![]() ,
,![]() ,
,![]() 的值;
的值;
(2)能否有99.9%把握認為注射此種疫苗對預防新型冠狀病毒有效?
附:![]() .
.
| 0.05 | 0.01 | 0.005 | 0.001 |
| 3.841 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知直線![]() 過橢圓
過橢圓![]() 的右焦點,且交橢圓于A,B兩點,線段AB的中點是
的右焦點,且交橢圓于A,B兩點,線段AB的中點是![]() ,
,
(1)求橢圓的方程;
(2)過原點的直線l與線段AB相交(不含端點)且交橢圓于C,D兩點,求四邊形![]() 面積的最大值.
面積的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,四棱錐E﹣ABCD的側棱DE與四棱錐F﹣ABCD的側棱BF都與底面ABCD垂直,AD⊥CD,AB∥CD,AB=3,AD=4,AE=5,![]() .
.
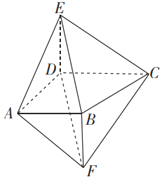
(1)證明:DF∥平面BCE.
(2)求A到平面BEDF的距離,并求四棱錐A﹣BEDF的體積.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com