
【題目】已知正項等比數(shù)列{an}滿足log2a1+log2a2+…+log2a2009=2009,則log2(a1+a2009)的最小值為 .
【答案】2
【解析】解:∵log2a1+log2a2+…+log2a2009=2009由對數(shù)的運算性質(zhì)可得,log2a1a2a2009=2009 ∴a1a2a2009=22009 ,
由等比數(shù)列的性質(zhì)可得,a1a2009=a2a2008=…=a10052 ,
∴a10052009=22009 ,
∵an>0,
∴a1005=2,
∴a1a2009=a2a2008=…=a10052=4,
由基本不等式可得,a1+a2009≥4,
則log2(a1+a2019)≥2即最小值2,
所以答案是:2.
【考點精析】關(guān)于本題考查的等比數(shù)列的通項公式(及其變式),需要了解通項公式:![]() 才能得出正確答案.
才能得出正確答案.


科目:高中數(shù)學 來源: 題型:
【題目】隨著互聯(lián)網(wǎng)的發(fā)展,移動支付(又稱手機支付)越來越普通,某學校興趣小組為了了解移動支付在大眾中的熟知度,對15-65歲的人群隨機抽樣調(diào)查,調(diào)查的問題是“你會使用移動支付嗎?”其中,回答“會”的共有![]() 個人.把這
個人.把這![]() 個人按照年齡分成5組:第1組
個人按照年齡分成5組:第1組![]() ,第2組
,第2組![]() ,第3組
,第3組![]() ,第4組
,第4組![]() ,第5組
,第5組![]() ,然后繪制成如圖所示的頻率分布直方圖.其中,第一組的頻數(shù)為20.
,然后繪制成如圖所示的頻率分布直方圖.其中,第一組的頻數(shù)為20.
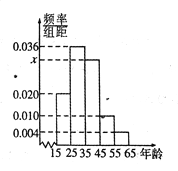
(1)求![]() 和
和![]() 的值,并根據(jù)頻率分布直方圖估計這組數(shù)據(jù)的眾數(shù);
的值,并根據(jù)頻率分布直方圖估計這組數(shù)據(jù)的眾數(shù);
(2)從第1,3,4組中用分層抽樣的方法抽取6人,求第1,3,4組抽取的人數(shù);
(3)在(2)抽取的6人中再隨機抽取2人,求所抽取的2人來自同一個組的概率.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】橢圓![]() :
:![]() 的左頂點為
的左頂點為![]() ,右焦點為
,右焦點為![]() ,上頂點為
,上頂點為![]() ,下頂點為
,下頂點為![]() ,若直線
,若直線![]() 與直線
與直線![]() 的交點為
的交點為![]() .
.
(1)求橢圓![]() 的標準方程;
的標準方程;
(2)點![]() 為橢圓
為橢圓![]() 的長軸上的一個動點,過點
的長軸上的一個動點,過點![]() 且斜率為
且斜率為![]() 的直線
的直線![]() 交橢圓
交橢圓![]() 于
于![]() 兩點,證明:
兩點,證明:![]() 為定值.
為定值.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】選修4-4:坐標系與參數(shù)方程
在極坐標系中,曲線![]() 的極坐標方程是
的極坐標方程是![]() ,以極點為原點
,以極點為原點![]() ,極軸為
,極軸為![]() 軸正半軸(兩坐標系取相同的單位長度)的直角坐標系
軸正半軸(兩坐標系取相同的單位長度)的直角坐標系![]() 中,曲線
中,曲線![]() 的參數(shù)方程為:
的參數(shù)方程為:![]() (
(![]() 為參數(shù)).
為參數(shù)).
(1)求曲線![]() 的直角坐標方程與曲線
的直角坐標方程與曲線![]() 的普通方程;
的普通方程;
(2)若用![]() 代換曲線
代換曲線![]() 的普通方程中的
的普通方程中的![]() 得到曲線
得到曲線![]() 的方程,若
的方程,若![]() 分別是曲線
分別是曲線![]() 和曲線
和曲線![]() 上的動點,求
上的動點,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】
某園藝公司種植了一批名貴樹苗,為了解樹苗的生長情況,從這批樹苗中隨機地測量了![]() 棵樹苗的高度(單位:厘米),并把這些高度列成如下的頻數(shù)分布表:
棵樹苗的高度(單位:厘米),并把這些高度列成如下的頻數(shù)分布表:
組別 |
|
|
|
|
|
|
頻數(shù) | 2 | 4 | 11 | 16 | 13 | 4 |
(Ⅰ)在這批樹苗中任取一棵,其高度在![]() 厘米以上的概率大約是多少?這批樹苗的平均高度大約是多少?
厘米以上的概率大約是多少?這批樹苗的平均高度大約是多少?
(Ⅱ)為了進一步獲得研究資料,標記![]() 組中的樹苗為
組中的樹苗為![]() ,
,![]() 組中的樹苗為
組中的樹苗為![]() ,現(xiàn)從
,現(xiàn)從![]() 組中移出一棵樹苗,從
組中移出一棵樹苗,從![]() 組中移出兩棵樹苗進行試驗研究,則
組中移出兩棵樹苗進行試驗研究,則![]() 組的樹苗
組的樹苗![]() 和
和![]() 組的樹苗
組的樹苗![]() 同時被移出的概率是多少?
同時被移出的概率是多少?
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】某食品廠定期購買面粉.已知該廠每天需用面粉6t,每噸面粉的價格為1800元,面粉的保管等其他費用為平均每噸每天3元,購面粉每次需支付運費900元.
(1)求該廠多少天購買一次面粉,才能使平均每天所支付的總費用最少?
(2)若提供面粉的公司規(guī)定:當一次購買面粉不少于210t時,其價格可享受9折優(yōu)惠(即原價的90%),問該廠是否考慮利用此優(yōu)惠條件?請說明理由.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】在物理實驗中,為了研究所掛物體的重量x對彈簧長度y的影響.某學生通過實驗測量得到物體的重量與彈簧長度的對比表:
物體重量(單位g) | 1 | 2 | 3 | 4 | 5 |
彈簧長度(單位cm) | 1.5 | 3 | 4 | 5 | 6.5 |
(1)畫出散點圖;
(2)利用公式(公式見卷首)求y對x的回歸直線方程;
(3)預測所掛物體重量為8g時的彈簧長度.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】[選修4-4:坐標系與參數(shù)方程]
以直角坐標系的原點![]() 為極點,
為極點,![]() 軸的正半軸為極軸,且兩個坐標系取相等的單位長度.已知直線
軸的正半軸為極軸,且兩個坐標系取相等的單位長度.已知直線![]() 的參數(shù)方程是
的參數(shù)方程是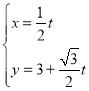 (
(![]() 為參數(shù)),曲線
為參數(shù)),曲線![]() 的極坐標方程是
的極坐標方程是![]() .
.
(1)寫出直線![]() 的普通方程和曲線
的普通方程和曲線![]() 的直角坐標方程;
的直角坐標方程;
(2)設(shè)直線![]() 與曲線
與曲線![]() 相交于
相交于![]() ,
,![]() 兩點,點
兩點,點![]() 為
為![]() 的中點,點
的中點,點![]() 的極坐標為
的極坐標為![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com