
若函數y=f(x)=x2-2x+4的定義域、值域都是閉區間[2,2b],求b的值.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:高中數學 來源: 題型:解答題
(12分)集合A是由具備下列性質的函數f(x)組成的:
①函數f(x)的定義域是[0,+∞);
②函數f(x)的值域是[-2,4);
③函數f(x)在[0,+∞)上是增函數,試分別探究下列兩小題:
(1)判斷函數f1(x)=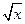 -2(x≥0)及f2(x)=4-6·
-2(x≥0)及f2(x)=4-6·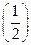 x(x≥0)是否屬于集合A?并簡要說明理由;
x(x≥0)是否屬于集合A?并簡要說明理由;
(2)對于(1)中你認為屬于集合A的函數f(x),不等式f(x)+f(x+2)<2f(x+1)是否對于任意的x≥0恒成立?若不成立,為什么?若成立,請說明你的結論.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
設f(x)是定義在R上的奇函數,且對任意實數x恒滿足f(x+2)=-f(x),當x∈[0,2]時,f(x)=2x-x2.
(1)求證:f(x)是周期函數.
(2)當x∈[2,4]時,求f(x)的解析式.
(3)計算f(0)+f(1)+f(2)+…+f(2011)
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
設函數f(x)=x2+x-.
(1)若函數的定義域為[0,3],求f(x)的值域;
(2)若定義域為[a,a+1]時,f(x)的值域是[-,],求a的值
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
(本小題12分)
如圖所示,將一矩形花壇ABCD擴建成一個更大的矩形花壇AMPN,要求M在AB的延長線上,N在AD的延長線上,且對角線MN過C點。已知AB=3米,AD=2米 。設
。設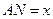 (單位:米),若
(單位:米),若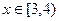 (單位:米),則當AM,AN的長度分別是多少時,花壇AMPN的面積最大?并求出最大面積。
(單位:米),則當AM,AN的長度分別是多少時,花壇AMPN的面積最大?并求出最大面積。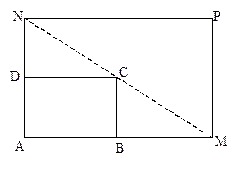
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
(本小題滿分12分)
某種型號的汽車在勻速行駛中每小時耗油量y (升)關于行駛速度x(千米/小時)的函數解析式可以表示為:
(升)關于行駛速度x(千米/小時)的函數解析式可以表示為: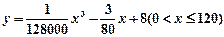 已知甲、乙兩地相距100千米。
已知甲、乙兩地相距100千米。
(Ⅰ)當汽車以40千米/小時的速度勻 速行駛時,從甲地到乙地要耗油多少升?
速行駛時,從甲地到乙地要耗油多少升?
(Ⅱ)當汽車以多大的速度勻速行駛時,從甲地到乙地耗油最少?最少為多少升?
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
設 ,
,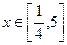 , 其中
, 其中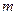 是不等于零的常數,
是不等于零的常數,
(1)、(理)寫出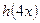 的定義域(2分);
的定義域(2分);
(文)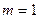 時,直接寫出
時,直接寫出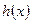 的值域(4分)
的值域(4分)
(2)、(文、理)求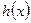 的單調遞增區間(理5分,文8分);
的單調遞增區間(理5分,文8分);
(3)、已知函數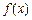
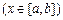 ,定義:
,定義: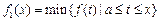
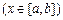 ,
,
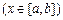 .其中,
.其中, 表示函數
表示函數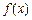 在
在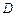 上的最小值,
上的最小值,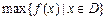 表示函數
表示函數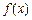 在
在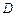
 上的最大值.例如:
上的最大值.例如: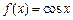 ,
,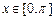 ,則
,則 ,
,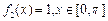 ,
,
(理)當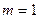 時,設
時,設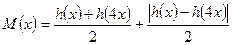 ,不等式
,不等式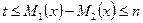
恒成立,求 的取值范圍(11分);
的取值范圍(11分);
(文)當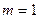 時,
時,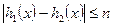 恒成立,求
恒成立,求 的取值范圍(8分);
的取值范圍(8分);
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
如圖,互相垂 直的兩條公路
直的兩條公路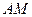 、
、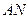 旁有一矩形花園
旁有一矩形花園 ,現欲將其擴建成一個
,現欲將其擴建成一個 更大的三角形花園
更大的三角形花園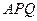 ,要求
,要求 在射線
在射線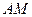 上,
上,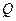 在射線
在射線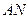 上,且
上,且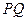 過點
過點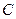 ,其中
,其中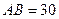 米,
米,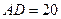 米. 記三角形花園
米. 記三角形花園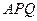 的面積為
的面積為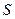 .
.
(1)設
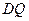
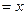 米,將
米,將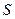 表示成
表示成 的函數.
的函數.
(2) 當
當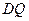 的長度是多少時,
的長度是多少時,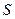 最小?并求
最小?并求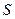 的最小值.
的最小值.
(3)要使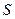 不小于
不小于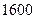 平方米,則
平方米,則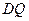 的長應在什么范圍內?
的長應在什么范圍內?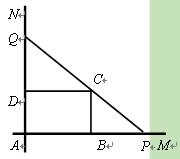
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com