
【題目】已知函數![]() ,
, ![]() .
.
(Ⅰ)當![]() 時,求函數
時,求函數![]() 切線斜率中的最大值;
切線斜率中的最大值;
(Ⅱ)若關于![]() 的方程
的方程![]() 有解,求實數
有解,求實數![]() 的取值范圍.
的取值范圍.
 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:
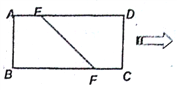
【題目】如圖,在矩形![]() 中,已知
中,已知![]() ,點
,點![]() 、
、![]() 分別在
分別在![]() 、
、![]() 上,且
上,且![]() ,將四邊形
,將四邊形![]() 沿
沿![]() 折起,使點
折起,使點![]() 在平面
在平面![]() 上的射影
上的射影![]() 在直線
在直線![]() 上.
上.
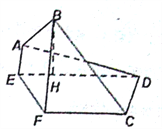
(I)求證: ![]() ;
;
(II)求點![]() 到平面
到平面![]() 的距離;
的距離;
(III)求直線![]() 與平面
與平面![]() 所成的正弦值.
所成的正弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知等比數列{an}滿足:|a2-a3|=10,a1a2a3=125.
(1) 求{an}的通項公式;
(2) 求證:![]() +
+![]() +…+
+…+![]() <1對任意正整數m都成立.
<1對任意正整數m都成立.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知{an}是等差數列,滿足a1=3,a4=12,數列{bn}滿足b1=4,b4=20,且{bn-an}為等比數列.
(1)求數列{an}和{bn}的通項公式;
(2)求數列{bn}的前n項和.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在添加劑的搭配使用中,為了找到最佳的搭配方案,需要對各種不同的搭配方式作比較.在試制某種牙膏新品種時,需要選用兩種不同的添加劑.現有芳香度分別為0,1,2,3,4,5的六種添加劑可供選用.根據試驗設計原理,通常首先要隨機選取兩種不同的添加劑進行搭配試驗.(寫解題過程)
(1)求所選用的兩種不同的添加劑的芳香度之和等于4的概率;
(2)求所選用的兩種不同的添加劑的芳香度之和不小于3的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】隨著人們經濟收入的不斷增長,個人購買家庭轎車已不再是一種時尚.車的使用費用,尤其是隨著使用年限的增多,所支出的費用到底會增長多少,一直是購車一族非常關心的問題.某汽車銷售公司做了一次抽樣調查,并統計得出某款車的使用年限![]() (單位:年)與所支出的總費用
(單位:年)與所支出的總費用![]() (單位:萬元)有如下的數據資料:
(單位:萬元)有如下的數據資料:
使用年限 | 2 | 3 | 4 | 5 | 6 |
總費用 | 2.2 | 3.8 | 5.5 | 6.5 | 7.0 |
若由資料知![]() 對
對![]() 呈線性相關關系.
呈線性相關關系.
(1)試求線性回歸方程![]() =
=![]()
![]() +
+![]() 的回歸系數
的回歸系數![]() ,
,![]() ;
;
(2)當使用年限為![]() 年時,估計車的使用總費用.
年時,估計車的使用總費用.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知直線![]() 的參數方程為
的參數方程為 為參數),以坐標原點為極點,
為參數),以坐標原點為極點, ![]() 軸的正半軸為極軸建立極坐標系,曲線
軸的正半軸為極軸建立極坐標系,曲線![]() 的極坐標方程為
的極坐標方程為![]() .直線
.直線![]() 過點
過點![]() .
.
(1)若直線![]() 與曲線
與曲線![]() 交于
交于![]() 兩點,求
兩點,求![]() 的值;
的值;
(2)求曲線![]() 的內接矩形的周長的最大值.
的內接矩形的周長的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】一片森林原面積為![]() .計劃從某年開始,每年砍伐一些樹林,且每年砍伐面積的百分比相等.并計劃砍伐到原面積的一半時,所用時間是10年.為保護生態環境,森林面積至少要保留原面積的
.計劃從某年開始,每年砍伐一些樹林,且每年砍伐面積的百分比相等.并計劃砍伐到原面積的一半時,所用時間是10年.為保護生態環境,森林面積至少要保留原面積的![]() .已知到今年為止,森林剩余面積為原面積的
.已知到今年為止,森林剩余面積為原面積的![]() .
.
(1)求每年砍伐面積的百分比;
(2)到今年為止,該森林已砍伐了多少年?
(3)為保護生態環境,今后最多還能砍伐多少年?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com