【題目】銷售甲、乙兩種商品所得利潤分別是
(單位：萬元)和
(單位：萬元)，它們與投入資金
(單位：萬元)的關系有經驗公式
，
. 今將
萬元資金投入經營甲、乙兩種商品，其中對甲種商品投資
(單位：萬元)，
（1）試建立總利潤
(單位：萬元)關于的函數關系式；
（2）當對甲種商品投資(單位：萬元)為多少時？總利潤(單位：萬元)值最大.
快樂小博士鞏固與提高系列答案科目：高中數學 來源： 題型：
【題目】設函數
的定義域為
，若存在閉區間
，使得函數滿足：①在
上是單調函數；②在 上的值域是
，則稱區間是函數 的“和諧區間”，
下列結論錯誤的是（ ）
A.函數 
存在 “和諧區間”
B.函數 
存在 “和諧區間”
C.函數 
不存在 “和諧區間”
D.函數 
存在 “和諧區間”
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】為了保護環境，發展低碳經濟，某單位在國家科研部門的支持下，進行技術攻關，采用新工藝，把二氧化碳轉化為一種可利用的化工產品.已知該單位每月的處理二氧化碳最少為400噸，最多為600噸，月處理成本
（元）與月處理量
（噸）之間的函數關系可近似的表示為：
，且每處理一噸二氧化碳得到可利用的化工產品價值為100元.
（1）若該單位每月成本支出不超過105000元，求月處理量的取值范圍；
（2）該單位每月能否獲利？如果獲利，求出最大利潤；如果不獲利，則國家至少需要補貼多少元才能使該單位不虧損？
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知點
，圓
：
，過點
的動直線
與圓
相交于
、
兩點，線段
的中點為
，且
在圓
上．
（1）若直線
（
）經過點
，求
的最大值；
（2）求圓
的方程；
（3）若過點
的直線
與圓
相交于
，
兩點，線段
的中點為
．
與
：
的交點為
，求證：
為定值．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數
，
（1）當
時，證明：函數
不是奇函數；
（2）判斷函數
的單調性，并利用函數單調性的定義給出證明；
（3）若是奇函數，且
在
時恒成立，求實數
的取值范圍.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】選修4-4：坐標系與參數方程
已知曲線C的極坐標方程是ρ=2cosθ，以極點為平面直角坐標系的原點，極軸為x軸的正半軸，建立平面直角坐標系，直線L的參數方程是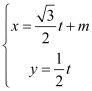
（t為參數）．
（1）求曲線C的直角坐標方程和直線L的普通方程；
（2）設點P（m，0），若直線L與曲線C交于A，B兩點，且|PA||PB|=1，求實數m的值。
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】面對某種流感病毒，各國醫療科研機構都在研究疫苗，現有A、B、C三個獨立的研究機構在一定的時期研制出疫苗的概率分別為
．求:
（1）他們能研制出疫苗的概率；
（2）至多有一個機構研制出疫苗的概率．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
