
�O(sh��)�E�AC: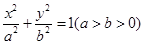 ���x����
���x����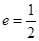 ���ҽ��c(di��n)��ֱ��
���ҽ��c(di��n)��ֱ��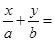 1�ľ��x
1�ľ��x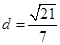 ��O������(bi��o)ԭ�c(di��n).
��O������(bi��o)ԭ�c(di��n).
��1����E�AC�ķ���;
��2���^�c(di��n)O���ɗl���ഹֱ���侀���c�E�AC�քe����A��B���c(di��n)���C���c(di��n)O��ֱ��AB�ľ��x�鶨ֵ��������AB�L�ȵ���Сֵ.
(1)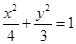 ;(2)
;(2)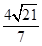 ��
��
����ԇ�}������
���}˼·��(1)�����x���ʼ��c(di��n)��ֱ���ľ��x��ʽ��⼴�ɣ���2���O(sh��)��ֱ�� ���̣�(li��n)��ֱ���c�E�A�ķ��̣��������P(gu��n)��
���̣�(li��n)��ֱ���c�E�A�ķ��̣��������P(gu��n)�� ��һԪ���η��̣�����
��һԪ���η��̣�����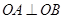 ���.
���.
Ҏ(gu��)�ɿ��Y(ji��)��ֱ���c�A�F������λ���P(gu��n)ϵ���}��һ��C���ԏ�(qi��ng).һ��˼·��(li��n)��ֱ���c�A�F�����ķ��̣��������P(gu��n)�� ��һԪ���η��̣����á��O(sh��)�����ķ����M(j��n)�����.
��һԪ���η��̣����á��O(sh��)�����ķ����M(j��n)�����.
ԇ�}��������1����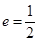 ��
��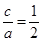 ����
����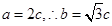
���ҽ��c(di��n)��ֱ��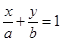 �ľ��x��
�ľ��x��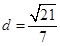
��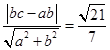 �����
�����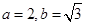 ��
��
���ԙE�AC�ķ��̞�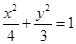 .
.
��2���O(sh��)A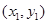 B
B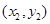
ֱ��AB�ķ��̞�y=kx+m�c�E�A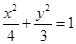 (li��n)����ȥy��
(li��n)����ȥy��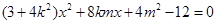
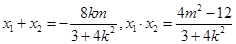
��OA��OB,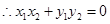
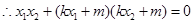
��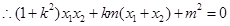
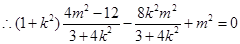
������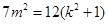
����O(sh��)��ֱ��AB�ľ��x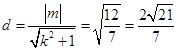
��OA��OB����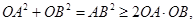
��(d��ng)�҃H��(d��ng)OA=OB�r(sh��)ȡ��=��
�� ��
��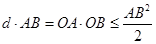
 .
.
���ҵ��L����Сֵ��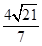 .
.
���c(di��n)��1.�E�A�Ę�(bi��o)��(zh��n)���̣�2.ֱ���c�E�A��λ���P(gu��n)ϵ.



| �꼉(j��) | �����n�� | �꼉(j��) | �����n�� |
| ��һ | ��һ���M(f��i)�n�����]�� | ��һ | ��һ���M(f��i)�n�����]�� |
| �߶� | �߶����M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
| ���� | �������M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�����}
��֪���タC��y2=2x��O������(bi��o)ԭ�c(di��n)����(j��ng)�^�c(di��n)M��2��0����ֱ��l�����タ��A��B���c(di��n)��P�钁�タC��һ�c(di��n)��
������ֱ��l��ֱ��x�S����|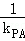 ��
��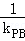 |��ֵ��
|��ֵ��
������������OAB����eS��ȡֵ������
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�����}
���x���҂��љE�A�Ľ����c�L�S���L��֮�ȼ�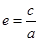 �������E�A���x����.��ɂ�(g��)�E�A���x����
�������E�A���x����.��ɂ�(g��)�E�A���x���� ��ͬ���Q�@�ɂ�(g��)�E�A����.
��ͬ���Q�@�ɂ�(g��)�E�A����.
��1�����E�A �c�E�A
�c�E�A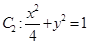 �Ƿ����ƣ����f�����ɣ�
�Ƿ����ƣ����f�����ɣ�
��2�����E�A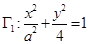
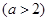 �c�E�A
�c�E�A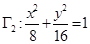 ���ƣ���
���ƣ��� ��ֵ��
��ֵ��
��3���O(sh��)��(d��ng)ֱ��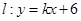 �c��2���еęE�A
�c��2���еęE�A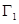 ����
���� ���c(di��n)��ԇ̽�����ڙE�A
���c(di��n)��ԇ̽�����ڙE�A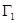 ���Ƿ���ڮ���
���Ƿ���ڮ��� �Ķ��c(di��n)
�Ķ��c(di��n)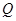 ��ʹ��ֱ��
��ʹ��ֱ��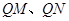 ��б��֮�e�鶨ֵ�������ڣ�������c(di��n)
��б��֮�e�鶨ֵ�������ڣ�������c(di��n)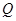 ������(bi��o)���������ڣ��f������.
������(bi��o)���������ڣ��f������.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�����}
��D,��ƽ��ֱ������(bi��o)ϵ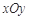 ��,
��,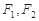 �քe�ǙE�A
�քe�ǙE�A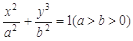 �����ҽ��c(di��n)����c(di��n)
�����ҽ��c(di��n)����c(di��n)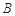 ������(bi��o)��
������(bi��o)�� ���B�Y(ji��)
���B�Y(ji��)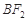 �����L���E�A���c(di��n)A���^�c(di��n)A��
�����L���E�A���c(di��n)A���^�c(di��n)A��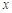 �S�Ĵ������E�A����һ�c(di��n)C���B�Y(ji��)
�S�Ĵ������E�A����һ�c(di��n)C���B�Y(ji��)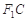 .
.
��1�����c(di��n)C������(bi��o)��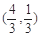 ,��
,��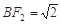 ,��E�A�ķ��̣�
,��E�A�ķ��̣�
��2����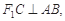 ��E�A�x����e��ֵ.
��E�A�x����e��ֵ.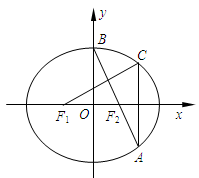
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�����}
�E�A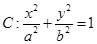
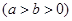 ���x���ʞ�
���x���ʞ�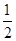 �������c(di��n)���c(di��n)
�������c(di��n)���c(di��n)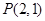 �ľ��x��
�ľ��x��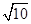 ��
��
(1) ��E�A �Ę�(bi��o)��(zh��n)���̣�
�Ę�(bi��o)��(zh��n)���̣�
(2) ��ֱ��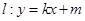 �c�E�A
�c�E�A �ཻ��
�ཻ�� ���c(di��n)(
���c(di��n)( ����������c(di��n))������
����������c(di��n))������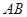 ��ֱ���ĈA�^�E�A
��ֱ���ĈA�^�E�A ������c(di��n)�����C��ֱ��
������c(di��n)�����C��ֱ��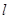 �^���c(di��n)�������ԓ���c(di��n)������(bi��o)��
�^���c(di��n)�������ԓ���c(di��n)������(bi��o)��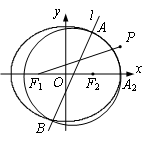
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�����}
��֪�E�AC��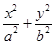 =1��a>0��b>0�����x�����c�p����
=1��a>0��b>0�����x�����c�p����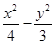 =1��һ�l�u������б�������ԭ�c(di��n)��A�ģ��E�A�Ķ̰��S�L��돽�ĈA�cֱ��sin
=1��һ�l�u������б�������ԭ�c(di��n)��A�ģ��E�A�Ķ̰��S�L��돽�ĈA�cֱ��sin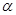 ��x+cos
��x+cos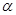 ��y��l=0����
��y��l=0���У�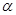 �鳣��(sh��)����
�鳣��(sh��)����
��1����E�AC�ķ��̣�
��2�����^�c(di��n)M��3��0����ֱ���c�E�AC�ཻTA��B���c(di��n)���O(sh��)P��E�A��һ�c(di��n)���ҝM��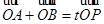 ��O������(bi��o)ԭ�c(di��n)������(d��ng)
��O������(bi��o)ԭ�c(di��n)������(d��ng)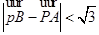 �r(sh��)����(sh��)��(sh��)tȡֵ������
�r(sh��)����(sh��)��(sh��)tȡֵ������
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�����}
��D��F(xi��n)��������ԭ�c(di��n)�����c(di��n)��x�S�ϵęE�AC���ҽ��c(di��n)��ֱ��l��x��4�ǙE�AC���Ҝ�(zh��n)����F(xi��n)��ֱ��l�ľ��x����3��
��1����E�AC�ķ��̣�
��2���c(di��n)P�ǙE�AC�τ�(d��ng)�c(di��n)��PM��l�������M���Ƿ�����c(di��n)P��ʹ�á�FPM����������Σ������ڣ�����c(di��n)P������(bi��o)���������ڣ�Ո(q��ng)�f�����ɣ�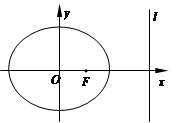
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�����}
��֪�E�AC�� ��
�� ��1(a>b>0)���x���ʞ�
��1(a>b>0)���x���ʞ�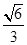 ���E�A���S��һ��(g��)���c(di��n)�c�ɂ�(g��)���c(di��n)��(g��u)�ɵ������ε���e��
���E�A���S��һ��(g��)���c(di��n)�c�ɂ�(g��)���c(di��n)��(g��u)�ɵ������ε���e��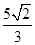 ��
��
(1)��E�AC�ķ��̣�
(2)��֪?ji��ng)�ֱ��y��k(x��1)�c�E�AC�ཻ��A��B���c(di��n)��
��������AB���c(di��n)�ęM����(bi��o)�飭 ����б��k��ֵ��
����б��k��ֵ��
����֪�c(di��n)M(��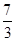 ��0)�����C��
��0)�����C��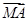 ��
��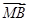 �鶨ֵ��
�鶨ֵ��
�鿴�𰸺ͽ���>>
���H�W(xu��)У��(y��u)�x - ����(x��)��(c��)�б� - ԇ�}�б�
����ʡ��(li��n)�W(w��ng)�`���Ͳ�����Ϣ�e��(b��o)ƽ�_(t��i) | �W(w��ng)���к���Ϣ�e��(b��o)���^(q��) | ����p�_�e��(b��o)���^(q��) | ��vʷ̓�o���x�к���Ϣ�e��(b��o)���^(q��) | �����֙�(qu��n)�e��(b��o)���^(q��)
�`���Ͳ�����Ϣ�e��(b��o)�Ԓ��027-86699610 �e��(b��o)�]�䣺58377363@163.com