【題目】已知函數
（
），
.
（1）若
，曲線
在點
處的切線與
軸垂直，求
的值；
（2）若
，試探究函數
與
的圖象在其公共點處是否存在公切線.若存在，研究
值的個數；，若不存在，請說明理由.
【答案】（1）
；（2）當
時，函數
與
的圖象在其公共點處不存在公切線，當
時，函數
與
的圖象在其公共點處存在公切線，且符合題意的
的值有且僅有兩個.
【解析】試題分析：（1）當
時， 
，得到
，依題意
，即可求解
的值；（2）假設
的圖象在其公共點
處存在公切線，分別求出導數，令
，得
，討論
，分別
， 
，令
，研究方程解的個數，可構造函數，運用都是求出單調區間，討論函數的零點個數即可判斷.
試題解析：（1）當
時， 
，∴ 
，
依題意得
，∴ 
.
（2）假設函數
與
的圖象在其公共點
處存在公切線，
∵
，∴ 
，∴ 
， 
，
由
得
，即
，
∴
，故
.
∵函數
的定義域為
，
當
時， 
，∴函數
與
的圖象在其公共點處不存在公切線；
當
時，令
，
∵
， 
，
∴
，即
（
）.
下面研究滿足此等式的
的值的個數：
設
，則
，且
，方程
化為
，
分別畫出
和
的圖象，
當
時， 
， 
，
由函數圖象的性質可得
和
的圖象有且只有兩個公共點（且均符合），
∴方程
有且只有兩個根.
綜上，當
時，函數
與
的圖象在其公共點處不存在公切線；當
時，函數
與
的圖象在其公共點處存在公切線，且符合題意的
的值有且僅有兩個.
點晴：本題主要考查了導數在函數中的綜合應用問題，其中解答中涉及到了利用導數求解曲線在某點處的切線方程，利用導數研究函數的單調性，利用函數的性質解決不等式、方程問題，著重考查了學生分析問題和解答問題的能力，以及推理與運算能力，本題的解答中認真審題，注意導數在函數中的合理應用，試題有一定的難度，屬于難題.
名校課堂系列答案科目：高中數學 來源： 題型：
【題目】定義在R上的偶函數f(x)滿足f(x＋1)＝－f(x)且f(x)在[－1,0]上是增函數，給出下列四個命題：
①f(x)是周期函數；②f(x)的圖象關于x＝1對稱；③f(x)在[1,2]上是減函數；④f(2)＝f(0)．
其中正確命題的序號是____________．(請把正確命題的序號全部寫出來)
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】一個幾何體的三視圖如圖所示，其中正視圖與側視圖是腰長為6的等腰直角三角形，俯視圖是正方形．
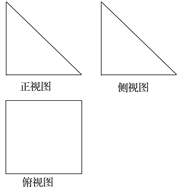
(1)請畫出該幾何體的直觀圖，并求出它的體積；
(2)用多少個這樣的幾何體可以拼成一個棱長為6的正方體ABCD—A1B1C1D1?如何組拼？試證明你的結論；
(3)在(2)的情形下，設正方體ABCD—A1B1C1D1的棱CC1的中點為E, 求平面AB1E與平面ABC所成二面角的余弦值．
查看答案和解析>>
科目：高中數學 來源： 題型：
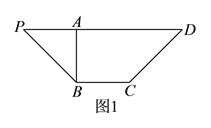
【題目】如圖
，等腰梯形
中， 
， 
于點
， 
，且
．沿
把
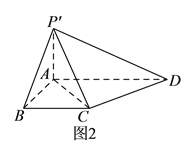
折起到
的位置（如圖
），使
．
（I）求證： 
平面
．
（II）求三棱錐
的體積．
（III）線段
上是否存在點
，使得
平面
，若存在，指出點
的位置并證明；若不存在，請說明理由．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某企業有甲、乙兩套設備生產同一種產品，為了檢測兩套設備的生產質量情況，隨機從兩套設備生產的大量產品中各抽取了50件產品作為樣本，檢測一項質量指標值，若該項質量指標值落在
內，則為合格品，否則為不合格品. 表1是甲套設備的樣本的頻數分布表，圖1是乙套設備的樣本的頻率分布直方圖.
表1：甲套設備的樣本的頻數分布表
質量指標值 | [95,100) | [100,105) | [105,110) | [110,115) | [115,120) | [120,125] |
頻數 | 1 | 4 | 19 | 20 | 5 | 1 |
圖1：乙套設備的樣本的頻率分布直方圖
（1）填寫下面列聯表，并根據列聯表判斷是否有90%的把握認為該企業生產的這種產品的質量指標值與甲、乙兩套設備的選擇有關；
